2.4. Kongruenzrechnung#
Bei der Division einer ganzen Zahl \(a\in\Z\) durch eine natürliche Zahl \(b\in\N\) haben wir in Modulare Arithmetik den Rest mit \(r = (a\bmod b)\) bezeichnet. Hierbei galt der Zusammenhang
Wir wollen im Folgenden eine weitere Bedeutung der Modulo-Operation einführen.
Definition 2.15 (Kongruenz modulo m)
Seien \(a,b,m\in\Z\) ganze Zahlen. Wir nennen \(\mathbf{a}\) kongruent \(\mathbf{b}\) modulo \(\mathbf{m}\), falls \(m\) ein Teiler der Differenz \(a-b\) ist, d.h, falls \(m\mid a-b\) gilt.
Wir schreiben in diesem Fall \(a\equiv b\bmod m\).
Wir machen nun allgemeine Beobachtungen um das Konzept der Kongruenz zu verdeutlichen.
Bemerkung 2.6 (Kongruenz und Teilbarkeit)
Es gilt \(a\equiv 0\bmod 2\), falls \(a \in \Z\) gerade ist und \(a\equiv 1\bmod 2\), falls \(a \in \Z\) ungerade ist.
Ergibt \(a \in \Z\) geteilt durch \(b\in\N\) den Divisionsrest \(r\in\N_0\), d.h. \(a=qb+r\), so ist \(a\) kongruent \(r\) modulo \(b\), d.h. es gilt \(a\equiv r\bmod b\).
Es gilt genau dann \(a\equiv 0\bmod b\), wenn \(b\) Teiler von \(a\) ist, d.h. es gilt \(b|a\).
Es gilt genau dann \(a\equiv b\bmod 0\), wenn \(a=b\) ist.
Allgemein gilt
\[a\equiv b\bmod m\quad\iff\quad a\equiv b\bmod (-m),\]weswegen man sich beim Modul \(m\) oft auf \(m\ge 0\) beschränkt.
Einige Grundaussagen über Kongruenzen sind in folgendem Satz zusammengestellt.
Satz 2.8 (Eigenschaften kongruenter ganzer Zahlen)
Sei \(m \in \N\) ein beliebiger Modul. Dann gelten die folgenden Aussagen:
Durch \(a\equiv b\bmod m\) wird für \(a,b \in \Z\) eine Äquivalenzrelation definiert. Die Äquivalenzklasse von \(a\) wird bei festem Modul \(m\) häufig mit \(\overline{a}\) bezeichnet, so dass gilt:
\[a\equiv b\bmod m \ \iff \ \overline{a}=\overline{b}.\]Die Menge der Äquivalenzklassen wird mit \(\Z/m\Z\) bezeichnet.
Ergibt die Division von \(a\in \Z\) durch \(m\) den Divisionsrest \(r \in \N_0\) mit \(0\le r<m\), so ist \(a\equiv r\bmod m\) und \(r\) ist der einzige Repräsentant der Äquivalenzklasse \(\overline{a}\) zwischen den natürlichen Zahlen \(0\) und \(m-1\), d.h. es gilt
\[\{r\} \ = \ \overline{a}\cap \{0,1,2,\dots,m-1\}.\]Diesen Divisionsrest haben wir zuvor mit \(r=(a\bmod m)\) bezeichnet.
Für \(a,b\in\Z\) gilt die Charakterisierung
\[a\equiv b\bmod m\quad\iff\quad (a\bmod m)=(b\bmod m).\]Als kanonische Repräsentanten der Äquivalenzklassen kann man die natürlichen Zahlen \(0,1,2,\dots,m-1 \in \N_0\) wählen, d.h. die Menge der Äquivalenzklassen ist charakterisiert durch
\[\Z/m\Z=\{\overline{0},\overline{1},\overline{2},\dots,\overline{m-1}\}\]und für die Mächtigkeit der Menge gilt \(|\Z/m\Z| = m\).
Die Äquivalenzrelation \(a\equiv b\bmod m\) ist mit Addition und Multiplikation verträglich, d.h. aus \(a_1\equiv a_2\bmod m\) und \(b_1\equiv b_2\bmod m\) folgt
\[a_1+b_1\equiv a_2+b_2\bmod m\quad\text{ und }\quad a_1\cdot b_1\equiv a_2\cdot b_2\bmod m.\]
Proof. In den Übungen zu zeigen. ◻
Die Menge der Äquivalenzklassen \(\Z/m\Z\) hat eine schöne algebraische Struktur, wie die folgende Bemerkung festhält.
Bemerkung 2.7 (Restklassenring \Z/m\Z)
Durch die Definition von Addition und Multiplikation als
wird die Menge der Äquivalenzklassen \(\Z/m\Z\) zu einem kommutativen Ring mit Nullelement \(\overline{0}\) und Einselement \(\overline{1}\), der als Restklassenring bezeichnet wird.
In der elementaren Zahlentheorie wird sehr oft mit Kongruenzen gerechnet, wie die folgende Beispiele belegen.
Beispiel 2.17 (Kongruenz ganzer Zahlen)
Wir beschäftigen uns mit der Frage wie man einer natürlichen Dezimalzahl \(n \in \N_0\) ansieht, ob sie durch \(3\) teilbar ist. Die Dezimalschreibweise \(n=(n_dn_{d-1}\dots n_1n_0)_{10}\) bedeutet gemäß der b-adischen Zahldarstellung in Definition 2.5
\[n \ = \ n_0+n_1\cdot 10+n_2\cdot 100+\dots+n_d\cdot 10^d,\]wobei \((d+1)\in\N\) die Stellenzahl von \(n\) darstellt.
Nun ist \(10\equiv 1\bmod 3\) und wegen der Verträglichkeit der Multiplikation in der Menge der Restklassen \(\Z/m\Z\) auch \(10^i\equiv 1\bmod 3\), d.h. es gilt
\[n\equiv n_0+n_1+\dots+n_d\bmod 3.\]Also ist die Dezimalzahl \(n \in \N_0\) genau dann durch \(3\) teilbar, wenn gilt
\[n\equiv n_0+\dots+n_d\equiv 0\bmod 3,\]d.h. wenn die Quersumme \(n_0+\dots+n_d\) durch \(3\) teilbar ist.
Auf gleiche Weise zeigt man die bekannten Teilbarkeitsregeln für die Zahlen \(9\) und \(11\).
Sei \(e=(111\dots 111)_{10}\) ein Exponent bestehend aus 100 Einsen in der Dezimaldarstellung. Wir fragen uns nun was die letzte Ziffer von \(3^e\) in der Dezimaldarstellung ist, d.h. uns interessiert also \(3^e\bmod 10\).
Es gilt
\[3^1\equiv 3\bmod 10,\quad 3^2\equiv 9\bmod 10,\quad 3^3\equiv 7\bmod 10,\quad 3^4\equiv 1\bmod 10.\]Wir schreiben den Exponenten als \(e=4q+r\), denn dann ist nämlich
\[3^e=3^{4q+r}=81^q\cdot 3^r\equiv 3^r\bmod 10.\]Nun ist
\[r\equiv e=100\cdot\text{Zahl} + 11\equiv 3\bmod 4,\]also \(r=3\) und somit folgt
\[3^e\equiv 3^r=3^3\equiv 7\bmod 10.\]Die letzte Ziffer von \(3^e\) ist also \(7\).
Durch Ausprobieren beobachtet man, dass für alle \(x,y\in\Z\) gilt:
\[x^2+y^2\equiv 0,1,2\bmod 4.\]Ist also \(n\in\N\) eine natürliche Zahl mit \(n\equiv 3\bmod 4\), so hat die quadratische diophantische Gleichung \(x^2+y^2=n\) keine ganzzahligen Lösungen \(x,y\in\Z\).
Das folgende Lemma beschreibt algebraische Unterstrukturen des Restklassenrings \(\Z/m\Z\) und ist daher oft hilfreich.
Lemma 2.7 (Kongruenz und Teilbarkeit)
Seien \(a,b\in\Z\) ganze Zahlen und seien \(d,m,n\in\N\) natürliche Zahlen.
Gilt \(a\equiv b\bmod m\) und \(d|m\), so gilt auch schon \(a\equiv b\bmod d\).
Gilt \(a\equiv b\bmod m\), \(a\equiv b\bmod n\) und \(\ggT(m,n)=1\), so folgt \(a\equiv b\bmod mn\).
Proof. Wir zeigen die beiden Aussagen im Folgenden getrennt.
Per Definition bedeutet \(a\equiv b\bmod m\), dass \(m|(a-b)\) gilt. Da \(d|m\) vorausgesetzt wurde, folgt sofort \(d|(a-b)\) und damit wiederum per Definition \(a\equiv b\bmod d\).
Die vorausgesetzten Kongruenzen bedeuten per Definition \(m|(a-b)\) und \(n|(a-b)\). Da \(\ggT(m,n)=1\) gilt sind die natürlichen Zahlen \(m,n\in\N\) teilerfremd und wegen Satz 2.3 folgt \(mn|(a-b)\) und damit per Definition schon die Behauptung.
◻
2.4.1. Invertierbarkeit modulo \(n\)#
Definition 2.16 (Multiplikativ Inverse modulo n)
Sei \(a\in\Z\) eine ganze Zahl und \(n\in\N\) ein Modul. Wir sagen \(a\) ist invertierbar modulo \(n\), falls eine ganze Zahl \(b\in\Z\) existiert mit \(ab\equiv 1\bmod n\). In diesem Fall nennt man die Zahl \(b\) eine multiplikativ Inverse von \(a\) modulo \(n\).
Es wird aus obiger Definition klar, dass die ganze Zahl \(0 \in \Z\) nicht invertierbar sein kann, da \(0 \cdot b = 0\) für alle \(b\in\Z\) gilt. Es sei angemerkt, dass es ausreicht alle kanonischen Repräsentanten \(\{1,\ldots n-1\}\) (die Zahl \(0\) scheidet trivialerweise aus) der Äquivalenzklassen des Restklassenrings \(\Z/n\Z\) nach einer potentiell zu \(a\in\Z\) multiplikativ inversen Zahl \(b\in\Z\) zu durchsuchen.
In Abhängigkeit des gewählten Modul \(n\in\N\) ist nicht jede ganze Zahl invertierbar, wie folgendes Beispiel zeigt.
Beispiel 2.18 (Multiplikativ Inverse modulo n)
Wir betrachten einige Beispiele für verschiedene Moduln \(n\in\N\) und untersuchen ganze Zahlen auf ihre multiplikative Invertierbarkeit.
Sei \(n:=4\). Dann gilt:
Wählen wir \(a:=-3\), so finden wir das multiplikativ inverse Element \(b = 3\), denn es gilt
Wählen wir hingegen \(a:=2\), so finden wir kein multiplikativ inverses Element \(b \in \{1,2,3\}\), so dass \(ab \equiv 1 \bmod 4\) gilt.
\[a\cdot b = -3 \cdot 3 = -9 \equiv 1 \bmod 4.\]
Sei nun \(n:=7\). Dann ist jede ganze Zahl \(a \in \Z/\{0\}\) invertierbar modulo \(n\). Dies sieht man ein, wenn man die kanonischen Repräsentanten der Äquivalenzklassen von \(\Z/n\Z\) (ohne die Null) betrachtet:
\(a := 1 \quad \Rightarrow \quad 1 \cdot 1 = 1 \equiv 1 \bmod 7\)
\(a := 2 \quad \Rightarrow \quad 2 \cdot 4 = 8 \equiv 1 \bmod 7\)
\(a := 3 \quad \Rightarrow \quad 3 \cdot 5 = 15 \equiv 1 \bmod 7\)
\(a := 4 \quad \Rightarrow \quad 4 \cdot 2 = 7 \equiv 1 \bmod 7\)
\(a := 5 \quad \Rightarrow \quad 5 \cdot 3 = 15 \equiv 1 \bmod 7\)
\(a := 6 \quad \Rightarrow \quad 6 \cdot 6 = 35 \equiv 1 \bmod 7\)
Wir sehen insbesondere, dass die Elemente \(a=1\) und \(a=6\) selbstinvers modulo \(7\) sind.
Folgendes Theorem gibt eine nützliche Äquivalenzbedingung zur Invertierbarkeit ganzer Zahlen \(a \in \Z\) modulo \(n\in\N\), die die Beobachtungen in Beispiel 2.18 erklären.
Satz 2.9 (Invertierbarkeit modulo n)
Sei \(a\in\Z\) eine ganze Zahl und \(n\in\N\) ein Modul.
Die Zahl \(a\) ist genau dann invertierbar modulo \(n\), wenn sie teilerfremd zum Modul \(n\) ist, d.h. wenn \(\ggT(n,a)=1\) gilt.
Ist \(\ggT(n,a)=1\) so findet man mit dem erweiterten euklidischen Algorithmus zwei ganzzahlige Lösungen \(x,y\in\Z\) der linearen diophantischen Gleichung \(xn+ya=1\). Dann gilt \(ya\equiv 1\bmod n\), d.h. \(y\) ist die multiplikativ Inverse zu \(a\) modulo \(n\).
Sei \(a\) invertierbar modulo \(n\) und seien \(b,b' \in \Z\) zwei multiplikative Inverse zu \(a\) modulo \(n\). Dann gilt \(b\equiv b'\bmod n\), d.h. bis auf ein Vielfaches des Modul \(n\in\N\) ist die multiplikativ Inverse von \(a\) eindeutig bestimmt.
Proof. Wir zeigen im Folgenden die einzelnen Aussagen des Theorems für \(a\in\Z\) und \(n\in\N\).
Für die Hinrichtung der Äquivalenzaussage nehmen wir an, dass \(a\) invertierbar modulo \(n\) ist. Dann gibt es per Definition eine ganze Zahl \(b\in\Z\) mit \(ab\equiv 1\bmod n\). Durch Umformen erkennen wir, dass \(ab-1 \equiv 0 \bmod n\) und somit ist \(n\mid ab-1\). Dies bedeutet, dass eine ganze Zahl \(k\in\Z\) existiert mit \(kn=ab-1\), d.h. \(-kn+ba=1\), woraus sofort \(\ggT(n,a)=1\) folgt.
Die Rückrichtung der Aussage folgt sofort aus der zweiten Aussage des Theorems.
Aus \(xn+ya=1\) folgt sofort \(ya\equiv 1\bmod n\), da \(xn\in\Z\) ein Vielfaches von \(n\in\N\) ist. Per Definition folgt dann aber schon, dass \(y\in \Z\) die multiplikativ Inverse zu \(a\) modulo \(n\) ist.
Aus \(ab\equiv 1\bmod n\) und \(ab'\equiv 1\bmod n\) folgt \(ab\equiv ab'\bmod n\). Also gilt \(n\mid (ab -ab')\) und somit \(n\mid a(b-b')\). Wegen \(\ggT(n,a)=1\) muss schon gelten \(n\mid (b-b')\), woraus schon die zu zeigende Aussage \(b\equiv b'\bmod n\) folgt.
◻
Aus der ersten Aussage von Satz 2.9 lässt sich leicht folgende wichtige Beobachtung ziehen.
Korollar 2.3 (Invertierbarkeit modulo p)
Wählt man als Modul eine Primzahl \(p \in \N\), so gilt für alle kanonischen Repräsentanten der Äquivalenzklassen \(a \in \{1,\ldots,p-1\}\) bereits \(\ggT(a,p) = 1\) und somit besitzen alle Elemente \(a \in \Z/p\Z\) eine multiplikativ Inverse modulo \(p\).
Wir erhalten somit die algebraische Struktur einer multiplikativen Gruppe in \(\Z/p\Z\).
Bemerkung 2.8 (Alternative Notation der multiplikativ Inversen)
Falls \(b\in\Z\) multiplikativ invers zu einer ganzen Zahl \(b\in\Z\) ist, d.h. es gilt \(ab\equiv 1\bmod m\), so findet man auch manchmal in der Literatur die Schreibweise
Die zweite Aussage von Satz 2.9 liefert uns eine Möglichkeit die multiplikativ Inverse \(b\in\Z\) modulo \(n\in\N\) einer ganzen Zahl \(a\in\Z\) mittels des erweiterten euklidischen Algorithmus zu berechnen.
Algorithmus 2.7 (Inversenberechnung von a modulo n)
Wir geben einen Algorithmus zur Berechnung einer multiplikativ Inversen modulo \(n\in\N\) zu einer ganzen Zahl \(a\in\Z\) an unter der Annahme, dass \(\ggT(a,n) = 1\) gilt.
\(n\in\N\) und \(a\in\Z\) mit \(\ggT(n,a)=1\) und \(0\le a\le n-1\) \(y\in\Z\) mit \(ya\equiv 1\bmod n\) und \(0\le y\le n-1\) Wende den erweiterter euklidischen Algorithmus auf \(n,a\) an. Man erhält \(x,y\in\Z\) mit \(xn+ya=1\) \(y\bmod n\)
Wir wollen den obigen Algorithmus an Hand eines einfachen Beispiels illustrieren.
Beispiel 2.19 (Berechnung der multiplikativ Inversen modulo n)
Sei \(a=37\) eine ganze Zahl und sei \(n=101\) ein Modul. Wir wenden zunächst den erweiterten euklidischen Algorithmus auf die Zahlen \(n\in\N\) und \(a\in\Z\) an und erhalten dadurch folgendes Schema:
\(q\) |
\(a_i\) |
\(x_i\) |
\(y_i\) |
101 |
1 |
0 |
|
37 |
0 |
1 |
|
2 |
27 |
1 |
-2 |
1 |
10 |
-1 |
3 |
2 |
7 |
3 |
-8 |
1 |
3 |
-4 |
11 |
2 |
1 |
11 |
-30 |
3 |
0 |
-37 |
101 |
Die Zahlen der vorletzten Zeile liefern uns hierbei die Lösung
Somit folgt
d.h. \(-30\) bzw. \(71\) ist multiplikativ invers zu \(37\) modulo \(101\).
Sind \(a\in\Z\) und der Modul \(n\in\N\) teilerfremd, d.h. es gilt \(\ggT(n,a)=1\), so bestimmen wir mit dem erweiterten euklidischen Algorithmus \(x,y\in\Z\) mit \(xn+ya=1\) in Algorithmus 2.7 um \(ya\equiv 1\bmod n\) zu erhalten. Der \(x\)-Wert wird hierbei gar nicht benötigt. Daher könnten wir auch beim erweiterten euklidischen Algorithmus darauf verzichten. Im Folgenden beschreiben wir eine mögliche Variante zur Inversenberechnung modulo \(n\).
Algorithmus 2.8 (Inversenberechnung modulo n (Variante II))
Wir geben einen Algorithmus zur Berechnung einer multiplikativ Inversen modulo \(n\in\N\) zu einer ganzen Zahl \(a\in\Z\) an unter der Annahme, dass \(\ggT(a,n) = 1\) gilt und unter Vermeidung der Variable \(x \in \Z\) im erweiterten euklidischen Algorithmus.
\(a,n\in\N\) mit \(\ggT(n,a)=1\) \(y\) mit \(ya\equiv 1\bmod n\) und \(0\le y\le n-1\) \(u\gets n\), \(v\gets a\), \(y\gets 0\), \(y'\gets 1\) \(q\gets \floor{\frac{u}{v}}\) \(u,v\gets v,u-qv\) \(y,y'\gets y',y-qy'\) \(y\bmod n\)
Ein entsprechende Implementierung in Python könnte wie folgt realisiert sein.
def invmod(a,n):
u,v,y,yy = n,a,0,1
while v>0:
q = u//v
u,v,y,yy = v,u-q*v,yy,y-q*yy
return y%n
2.4.2. Die Eulersche \(\varphi\)-Funktion#
Wir definieren zunächst einen wichtigen Begriff aus der Algebra.
Definition 2.17 (Einheit)
Sei \(R\) ein Ring mit neutralem Element \(1\) bezüglich der Multiplikation. Wir nennen dann ein Element \(u\in R\) Einheit (im Englischen: unit), falls es ein multiplikativ Inverses besitzt, d.h. falls ein Element \(v\in R\) existiert, so dass
Die Menge der Einheiten eines Rings bildet eine Gruppe bezüglich der Multiplikation (die insbesondere abgeschlossen ist), die häufig mit \(R^{\ast}\) (also als \((\Z/m\Z)^\ast\) im Falle des Restklassenrings) bezeichnet wird.
Wir betrachten nun einen festen Modul \(m\in \N\) und eine ganze Zahl \(a\in \Z\). Wir wollen im Folgenden untersuchen wann die Äquivalenzklasse \(\overline{a} \in \Z/m\Z\) von \(a\) eine Einheit, also ein Element von \((\Z/m\Z)^\ast\) ist. Wir stellen mit Hilfe von Satz 2.9 fest, dass gilt:
Wir erkennen also, dass die Äquivalenzklasse \(\overline{a}\) genau dann eine Einheit in \(\Z/m\Z\) ist, wenn \(\ggT(a,m)=1\) gilt. Wir fassen dieses Ergebnis im folgenden Korollar zusammen.
Korollar 2.4 (Charakterisierung von Einheiten im Restklassenring)
Für die Einheiten des Restklassenrings \(\Z/m\Z\) gilt:
Wir geben im Folgenden die Einheiten für einige Restklassenringe mit kleinen Moduln explizit an.
Beispiel 2.20 (Einheiten des Restklassenrings)
Die Einheiten der Restklassenringe \(\Z/m\Z\) für die Moduln \(0 \leq m \leq 10\) lassen sich in folgender Tabelle festhalten.
\(m\) |
Repräsentanten von \((\Z/m\Z)^\ast\) |
0 |
0 |
1 |
0 |
2 |
1 |
3 |
1, 2 |
4 |
1, 3 |
5 |
1, 2, 3, 4 |
6 |
1, 5 |
7 |
1, 2, 3, 4, 5, 6 |
8 |
1, 3, 5, 7 |
9 |
1, 2, 4, 5, 7, 8 |
10 |
1, 3, 7, 9 |
Wir definieren uns nun eine sehr hilfreiche Funktion, die die Anzahl der Einheiten in einem Restklassenring modulo \(n\in\N\) angibt.
Definition 2.18 (Eulersche \varphi-Funktion)
Wir definieren die Eulersche \(\mathbf{\varphi}\)-Funktion (manchmal auch als Totient von \(n\) bezeichnet) durch
Die Entwicklung der Eulerschen \(\varphi\)-Funktion lässt sich in folgender Tabelle angeben:
\(n\) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
\(\varphi(n)\) |
1 |
1 |
2 |
2 |
4 |
2 |
6 |
4 |
6 |
4 |
10 |
4 |
12 |
6 |
8 |
8 |
16 |
6 |
18 |
8 |
Die Werte der Eulerschen \(\varphi\)-Funktion sind in folgender Abbildung für \(1 \leq n \leq 1000\) geplottet [Bat09].
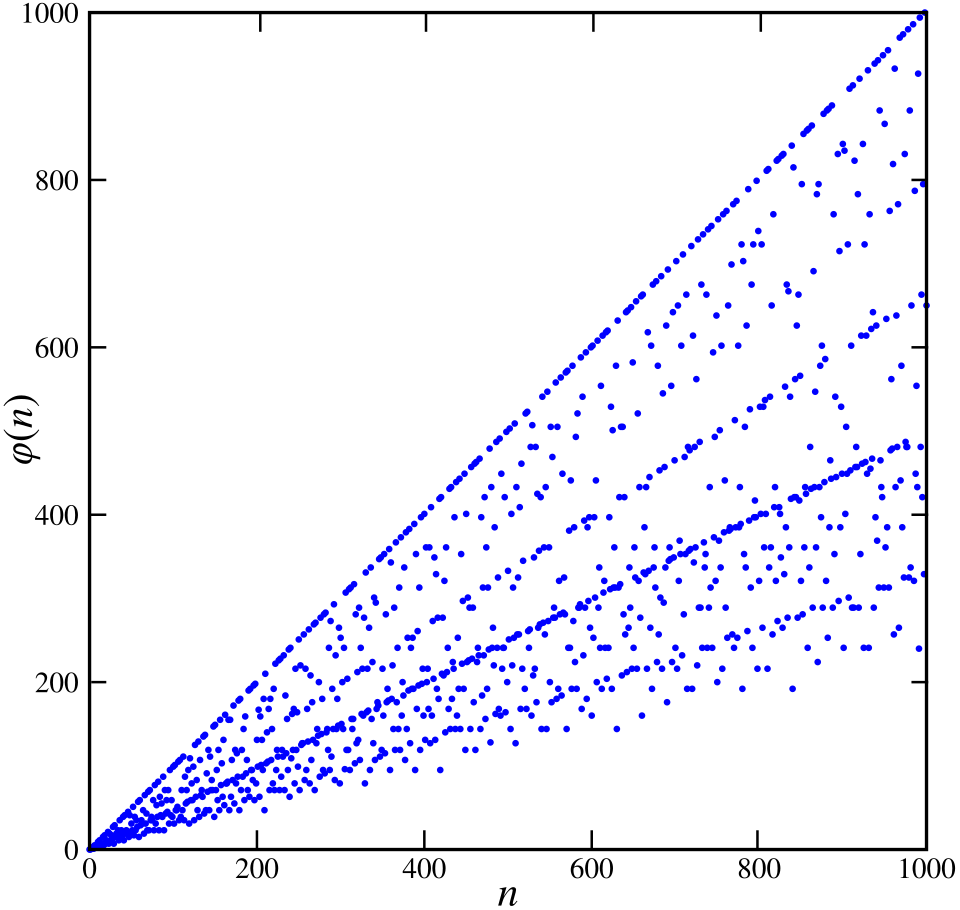 {width=“70%“}
{width=“70%“}
Das folgende Theorem stellt einen wichtigen Zusammenhang zwischen Primzahlen und der Eulerschen \(\varphi\)-Funktion her und gibt Voraussetzungen für eine zusätzliche algebraische Struktur an.
Satz 2.10 (Körpereigenschaft eines Restklassenrings)
Für einen Modul \(n\in\N\) gelten die folgenden Äquivalenzen:
Proof. Für \(n=1\) sind alle drei Aussagen falsch und daher die Behauptung des Satzes korrekt. Daher können wir ohne Einschränkungen im Folgenden \(n\ge 2\) voraussetzen.
Wegen \(n\ge 2\) ist \(\overline{0}\not\in (\Z/n\Z)^\ast\). Also gilt schon mal
\[(\Z/n\Z)^\ast \subseteq \{ \overline{1},\overline{2},\dots,\overline{n-1}\}\quad\text{ und damit }\quad \varphi(n)\le n-1.\]Wir stellen nun fest, dass \(\varphi(n)=n-1\) genau dann gilt, wenn alle Zahlen zwischen \(1\) und \(n-1\) teilerfremd zu \(n\) sind. Dies ist aber äquivalent dazu, dass \(n\) keinen nichttrivialen Teiler zwischen \(2\) und \(n-1\) hat, was aber gleichwertig damit ist, dass \(n\) eine Primzahl ist.
Der Restklassenring \(\Z/n\Z\) ist genau dann ein Körper, wenn sich alle Elemente außer der \(\overline{0}\) multiplikativ invertieren lassen. Dies ist genau dann der Fall, wenn
\[|(\Z/n\Z)^{\ast}| \ = \ |(\Z/n\Z)-1| \ = \ n-1.\]Dies gilt nach der ersten Aussage des Satzes genau dann, wenn \(n\) eine Primzahl ist.
◻
Bemerkung 2.9 (Algebraische Interpretation)
Ist \(p\in\N\) eine Primzahl, so schreiben wir statt \(\Z/p\Z\) auch häufig für den endlichen Körper \(\F_p\) (im Englischen: field).
Ist \(n\) keine Primzahl, also ist \(n=ab\) mit \(1<a,b<n\), so gilt in \(\Z/n\Z\) natürlich \(\overline{a}\cdot \overline{b}=\overline{0}\) für \(\overline{a}\ne \overline{0}\) und \(\overline{b}\ne \overline{0}\), d.h. \(\Z/n\Z\) ist in diesem Fall kein Integritätsring.
Die Eulersche \(\varphi\)-Funktion weist besondere Eigenschaften auf, wie folgendes Theorem aussagt.
Satz 2.11 (Eigenschaften der Eulerschen \varphi-Funktion)
Für die Eulersche \(\varphi\)-Funktion gelten die folgenden Aussagen:
Seien \(m,n \in \N\) natürliche Zahlen. Dann gilt
\[\ggT(m,n)=1 \quad \Longrightarrow \quad \varphi(mn)=\varphi(m) \cdot \varphi(n).\]Zahlentheoretische Funktionen mit dieser Eigenschaft nennt man multiplikativ.
Für die Primfaktorzerlegung \(n=p_1^{e_1}\dots p_r^{e_r}\) mit paarweise verschiedenen Primzahlen \(p_i\) und positiven Exponenten \(e_i\ge 1\) gilt:
\[\varphi(n) \ = \ \prod_i p_i^{e_i-1}(p_i-1) \ = \ n(1-\frac{1}{p_1})\dots (1-\frac{1}{p_r}) \ = \ n\prod_{p|n}(1-\frac{1}{p}).\]
Proof. 1. Dies wird später mit Hilfe des chinesischen Restssatzes bewiesen werden.
Für eine Primzahl \(p\) und \(e\ge 1\) gilt
\[\begin{aligned} %TODO Verstehen und intuitiv erklären! \{0\le a\le p^e-1:\ggT(a,p^e)=1\}&=& \{0\le a\le p^e-1:\ggT(a,p)=1\}=\\ &=&\{a\in\Z \: : \: 0\le a\le p^e-1\}\setminus \{pb \in \Z \: : \: 0\le b\le p^{e-1}-1\}. \end{aligned}\]Hieraus folgt nun
\[\varphi(p^e) \: = \: p^e-p^{e-1} \: = \: p^{e-1}(p-1) \: = \: p^e(1-\frac{1}{p}).\]Mit der ersten Aussage dieses Theorems zur Multiplikativität der Eulerschen \(\varphi\)-Funktion ergibt sich daraus die Behauptung
\[\begin{aligned} \varphi(n)&=&\varphi(\prod_i p_i^{e_i}) \: = \: \prod_i \varphi(p_i^{e_i}) \: = \: \prod_i p_i^{e_i-1}(p_i-1)\\ &=& \prod_i p_i^{e_i}(1-\frac{1}{p_i}) \: = \: n \prod_i(1-\frac{1}{p_i}). \end{aligned}\]
◻
Der letzte Satz zeigt, dass man den Wert der Eulerschen \(\varphi\)-Funktion für eine natürliche Zahl \(n\in\N\) leicht berechnen kann, wenn man die Primfaktorzerlegung von \(n\) kennt. Dies macht sie praktisch nicht effizient anwendbar für große Zahlen nach unseren Beobachtungen in Bemerkung 2.4. Leider ist bis heute keine andere Berechnungsmöglichkeit bekannt.
2.4.3. Lineare Gleichungen im Restklassenring#
In diesem Abschnitt interessieren wir uns für lineare Gleichungen im Restklassenring \(\Z/m\Z\) der Form
wobei \(a,b \in \Z\) ganze Zahlen sind und \(m \in \N\) ein fest gewählter Modul ist. Wir wollen also verstehen, ob beispielsweise die Gleichung \(6x \equiv 4 \bmod 10\) Lösungen im Restklassenring \(\Z/10\Z\) besitzt.
Das folgende Theorem gibt uns glücklicherweise ein Kriterium zur Lösbarkeit solcher linearer Gleichungen und charakterisiert die Lösungsmengen.
Satz 2.12 (Lösbarkeit von linearen Gleichungen im Restklassenring)
Seien \(a,b\in\Z\) ganze Zahlen und sei \(m\in\N\) ein fester Modul. Mit dem erweiterten euklidischen Algorithmus findet man nach Satz 2.5 zwei ganze Zahlen \(u,v\in\Z\), so dass die lineare diophantische Gleichung \(au+mv=\ggT(a,m)\) erfüllt ist. Dann gelten die folgenden Aussagen:
Die lineare Gleichung \(ax\equiv b\bmod m\) ist genau dann lösbar, wenn \(\ggT(a,m) \mid b\) gilt.
Gilt \(\ggT(a,m)\mid b\), so erfüllt
\[x_0 \: = \: \frac{b}{\ggT(a,m)}u\]die Gleichung \(ax_0\equiv b\bmod m\).
Gilt \(ax_0\equiv b\bmod m\) für ein \(x_0 \in \Z\), so ist die Lösungsmenge der linearen Gleichung gegeben durch
\[\{x\in\Z: ax\equiv b\bmod m\} \ = \ \{x_0 + i\cdot \frac{m}{\ggT(a,m)}: i\in\Z\}.\]Gilt \(\ggT(a,m)\mid b\), so gibt es genau \((\ggT(a,m) \bmod m) \in \N\) verschiedene Lösungen \(x \in \Z/m\Z\) der Gleichung \(ax\equiv b\bmod m\), z.B.
\[x_0+i\frac{m}{\ggT(a,m)}\quad\text{ für }\quad i=0,\dots,\ggT(a,m)-1,\]wenn \(x_0\) eine Lösung der Gleichung ist.
Proof. Wir zeigen die Aussagen des Theorems im Folgenden.
Hinrichtung: Nehmen wir an, dass eine Lösung \(x\in\Z\) der linearen Gleichung \(ax\equiv b\bmod m\) existiert, so gibt es eine ganze Zahl \(y\in\Z\) mit \(ax=b+my\). Da \(\ggT(a,m)\) die Zahlen \(ax\) und \(by\) teilt, folgt bereits die Behauptung \(\ggT(a,m)|b\).
Rückrichtung: Die Umkehrung der Aussage wird an einer späteren Stelle separat gezeigt.Die Voraussetzung \(\ggT(a,m)\mid b\) liefert, dass \(\frac{b}{\ggT(a,m)} \in \Z\) eine ganze Zahl ist. Es folgt dann
\[ax_0 \: \: \frac{abu}{\ggT(a,m)} \: = \: \frac{b(\ggT(a,m)-mv)}{\ggT(a,m)} \: = \: b - \frac{b}{\ggT(a,m)} mv.\]Nehmen wir nun beide Seiten der Gleichung modulo \(m\) führt dies zu der gewünschten Aussage \(ax_0\equiv b\bmod m\).
Wir zeigen zunächst die Inklusion \(\subseteq\). Sei \(x\in\Z\) eine Lösung der linearen Gleichung \(ax\equiv b\bmod m\). Es folgt wegen der Voraussetzung \(ax\equiv ax_0\bmod m\), also per Definition \(m\mid a(x-x_0)\). Teilen wir beide Zahlen nun durch \(\ggT(a,m)\) so erhalten wir
\[\frac{m}{\ggT(a,m)} \mid \frac{a}{\ggT(a,m)} (x-x_0).\]Wegen \(\ggT( \frac{a}{\ggT(a,m)}, \frac{m}{\ggT(a,m)})=1\) erhält man schon \(\frac{m}{\ggT(a,m)} \mid (x-x_0)\), also gibt es eine ganze Zahl \(i\in\Z\) mit
\[x-x_0=i\cdot \frac{m}{\ggT(a,m)} \quad \iff \quad x = x_0 + i\cdot \frac{m}{\ggT(a,m)},\]was die erste Inklusion zeigt.
Wir zeigen nun die umgekehte Inklusion \(\supseteq\). Es sei \(i \in \Z\) beliebig und \(x := x_0+i\frac{m}{\ggT(a,m)}\). Dann gilt\[a\left(x_0+i\frac{m}{\ggT(a,m)}\right) = ax_0+i\frac{a}{\ggT(a,m)}m \equiv ax_0\equiv b\bmod m.\]Somit ist das gewählte \(x \in \Z\) für alle \(i \in \Z\) eine Lösung der linearen Gleichung, was die gewünschte Inklusion zeigt.
Nach der vorigen Aussage des Theorems sind die Zahlen \(x_i=x_0+i\frac{m}{\ggT(a,m)}\) für alle \(i\in\Z\) genau die Menge der ganzzahligen Lösungen der Gleichung \(ax\equiv b\bmod m\). Wir müssen nun noch untersuchen wann zwei Lösungen \(x_i, x_j \in \Z\) gleich modulo \(m\) sind. Hierzu betrachten wir:
\[\begin{aligned} x_i\equiv x_j\bmod m &\iff& i\frac{m}{\ggT(a,m)} \: \equiv \: j\frac{m}{\ggT(a,m)} \bmod m\\ &\iff& m\mid (i-j)\frac{m}{\ggT(a,m)} \quad\iff\quad \ggT(a,m) m \mid (i-j)m\\ &\iff& \ggT(a,m)\mid i-j \quad\iff\quad i\equiv j\bmod \ggT(a,m). \end{aligned}\]Damit folgt schon die Behauptung.
◻
Wir betrachten nun ein Beispiel, dass die Lösungen von linearen Gleichungen im Restklassenring untersucht.
Beispiel 2.21 (Lösungen linearer Gleichungen im Restklassenring)
Wir untersuchen im Folgenden zwei verschiedene lineare Gleichungen im Restklassenring \(\Z/10\Z\).
Wir betrachten zunächst die lineare Gleichung \(6x\equiv 4\bmod 10\). Nach den Aussagen von Satz 2.12 existieren genau \((\ggT(6,10) \bmod 10) = 2\) verschiedene Lösungen, da \(\ggT(6,10) \mid 4\) gilt. Wir wollen diese Lösungen nun durch Ausprobieren in folgender Tabelle finden:
\(x\)
\(ax\)
\(ax \bmod b\)
0
0
0
1
6
6
2
12
2
3
18
8
4
24
4
5
30
0
6
36
6
7
42
2
8
48
8
9
54
4
Wir sehen also, dass die lineare Gleichung die beiden Lösungen \(4\) und \(9\) modulo \(10\) besitzt.
Nun untersuchen wir die lineare Gleichung \(6x\equiv 5\bmod 10\). Nach den Aussagen von Satz 2.12 existieren keine Lösungen \(x \in \Z\), da \(\ggT(6,10) \nmid 5\) gilt. Dies lässt sich leicht an der obigen Tabelle verifizieren, da dort kein Rest \(5\) modulo \(10\) entsteht.
Oft sind auch die einfachen Aussagen des folgenden Satzes hilfreich, die eine Beziehung zwischen Lösungen verschiedener linearer Gleichungen herstellen.
Satz 2.13 (Beziehungen linearer Gleichungen in Restklassenringen)
Seien \(a,b\in\Z\) zwei ganze Zahlen und \(m\in\N\) ein fest gewählter Modul. Dann gelten die folgenden Aussagen:
Sei \(d=\ggT(a,b,m)\) der größte gemeinsame Teiler der drei Zahlen \(a,b\) und \(m\). Schreibt man \(a=da'\), \(b=db'\), \(m=dm'\), so gilt \(\ggT(a',b',m')=1\) und für beliebige ganze Zahlen \(x\in\Z\) hat man die folgende Äquivalenz der Lösungsmengen:
\[ax\equiv b\bmod m\quad\iff\quad a'x\equiv b'\bmod m'.\]Gilt \(\ggT(a,m)=1\) und ist \(a^{-1} \in \Z\) invers zu \(a\) modulo \(m\), d.h. \(a^{-1}a\equiv 1\bmod m\), so hat man die folgende Äquivalenz:
\[ax\equiv b\bmod m\quad\iff\quad x\equiv a^{-1}b\bmod m.\]Gilt \(\ggT(a,m)>1\) und \(\ggT(a,m)\nmid b\), so hat die Gleichung \(ax\equiv b\bmod m\) keine Lösungen.
Proof. Wir zeigen im Folgenden die Aussagen des Theorems.
Man kann direkt aus der Definition der Kongruenz ganzer Zahlen folgern, dass gilt:
\[\begin{aligned} ax\equiv b\bmod m &\iff& m\mid ax-b \quad\iff\quad dm'\mid da'x-db'\\ &\iff& m'\mid a'x-b' \quad\iff\quad a'x\equiv b'\bmod m'. \end{aligned}\]Zeigen wir zunächst die Hinrichtung, so gilt:
\[ax\equiv b\bmod m \quad \Longrightarrow \quad a^{-1}ax\equiv a^{-1}b\bmod m \quad\iff\quad x\equiv a^{-1}b\bmod m\]Für die Rückrichtung gehen wir analog vor mit:
\[x\equiv a^{-1}b\bmod m \quad \Longrightarrow \quad ax\equiv aa^{-1}b\bmod m \quad\iff\quad ax\equiv b\bmod m,\]woraus die Behauptung folgt.
Die Aussage haben wir bereits in Satz 2.12 bewiesen.
◻
