3.1. Substitutionschiffren

Wir beschäftigen uns zunächst mit sogenannten Substitutionschiffren bei denen jeder Buchstabe des Klartexts durch ein anderes Zeichen ersetzt (d.h. substitutiert) wird. Hierbei wird jedoch die Position des Zeichens innerhalb des Chiffretexts nicht verändert.

3.1.1. CAESAR-Verschlüsselung

Wir betrachten zunächst das einführende Beispiel der CAESAR-3-Verschlüsselung aus Algorithmus 1.1. Dieses lässt sich durch eine geeignete Parametrisierung und die Verwendung der Modulo-Operation in Modulare Arithmetik leicht verallgemeinern.

Algorithmus 3.1 (CAESAR-Verschlüsselung)

1. Wir wählen als zu Grunde liegendes Alphabet \(\Sigma\) die lateinischen Großbuchstaben (ohne deutsche Umlaute) A,…,Z und nutzen als Klartext- und Chiffretextraum \(\mathcal{P} = \mathcal{C} = \Sigma^*\), d.h. die Menge aller Wörter über dem Alphabet \(\Sigma\).

2. Als Schlüsselraum wählen wir die Menge der ganzen Zahlen \(\mathcal{K} = \Z\). Ein Schlüssel \(k \in \mathcal{K}\) besteht also lediglich aus einer gewählten ganzen Zahl. Die Größe des Schlüsselraums \(|\mathcal K|\) entspricht der Größe des gewählten Alphabets \(|\Sigma|\).

3. Wir definieren eine durch den Schlüssel \(k \in \mathcal{K}\) parametrisierte Verschlüsselungsfunktion \(f_k\) wie folgt:

   \[f_k(x) \ := \ x + k \bmod 26,\]

   wobei \(x+k\bmod 26\) den Rest der Division von \(x+k\) durch \(26\) bezeichnet, der per Definition zwischen \(0\) und \(25\) liegt. \(f_k\) realisiert also eine zyklische Verschiebung des Alphabets um \(k\in\Z\) Stellen.

4. Verschlüsselung: Ein Klartext \(m \in \mathcal{P}\) mit \(m = a_1a_2a_3\dots\) wird verschlüsselt, indem man jeden Buchstaben \(a_i \in \Sigma\) des Textes sukzessiv durch \(f_k(a_i) \in \Sigma\) mittels obiger Verschlüsselungsfunktion ersetzt. Somit erhält man also den Chiffretext \(c \in \mathcal{C}\) mit

   \[c = f_k(a_1)f_k(a_2)f_k(a_3)\dots.\]

5. Entschlüsselung: Die Entschlüsselung eines Chiffretexts \(c = c_1,c_2,c_3,\dots\) funktioniert analog wie die Verschlüsselung, nur dass man statt \(f_k\) die Umkehrfunktion \(f_k^{-1}\) verwendet, d.h.

   \[m = f_k^{-1}(c_1)f_k^{-1}(c_2)f_k^{-1}(c_3)\dots\]

   Die Umkehrfunktion \(f^{-1}\) erhält man direkt, wenn man direkt indem man das Vorzeichen des Schlüssels \(k \in \Z\) umkehrt und als Parameter der Verschlüsselungsfunktion nutzt, d.h. es gilt

   \[f_k^{-1} \ = \ f_{-k}.\]

Wir wollen das Prinzip der verallgemeinertern CAESAR-Verschlüsselung kurz an einem Beispiel illustrieren.

Beispiel 3.1 (CAESAR-Verschlüsselung)

Mit Hilfe der in Algorithmus 3.1 eingeführten CAESAR-Verschlüsselung und dem gewählten Schlüssel \(k=37\) wird der Klartext

WIR BEGINNEN GANZ LEICHT

zum folgenden Chiffretext verschlüsselt:

HTC MPRTYYPY RLYK WPTNSE

Nutzt man nun den Schlüssel \(k=-37\) und wendet wiederum die CAESAR-Verschlüsselung an, so erhält man den ursprünglichen Klartext zurück.

Natürlich überträgt sich die CAESAR-Verschlüsselung auch auf andere Alphabete \(\Sigma\). Beispielsweise kann man Dateien CAESAR-verschlüsseln, wenn man die Datei als Bytefolge \(a_1,a_2,a_3,\dots\) auffasst mit \(0\le a_i\le 255\) und die folgende Verschlüsselungsfunktionen verwendet:

\[f_k(x)=x+k\bmod 256\]

Hierdurch erweitert sich der Schlüsselraum auf 256 mögliche Schlüssel.

Wir wollen im Folgenden noch kurz die Sicherheit des CAESAR-Kryptosystems diskutieren.

Bemerkung 3.1 (Kryptoanalyse für CAESAR-Verschlüsselung)

1. Es handelt sich bei der CAESAR-Verschlüsselung um ein symmetrisches Kryptosystem, das auf einer einfachen Blockchiffrierung für Blöcke der Größe 1 basiert.

2. Haben \(k_1 \in \Z\) und \(k_2 \in \Z\) den gleichen Divisionsrest bei der Division durch \(26\), d.h. gilt \(k_1\bmod 26=k_2\bmod 26\), so gilt \(f_{k_1}=f_{k_2}\). Daher gibt es eigentlich nur 26 verschiedene Schlüssel dieser CAESAR-Verschlüsselung, was ein einfaches Durchprobieren der möglichen Klartexte ermöglicht. Vermutet man, dass die aus Großbuchstaben bestehende, verschlüsselte Nachricht \(c \in \mathcal{C}\) CAESAR-verschlüsselt wurde, so kann man für alle Schlüssel \(k\in \{0,1,\dots,25\}\) den möglichen Klartext \(m = f_{-k}(c)\) bestimmen und prüfen, ob etwas Sinnvolles dabei herauskommt.

Wir wollen das Brechen der CAESAR-Verschlüsselung mit einem einfachen Beispiel kurz illustrieren.

Beispiel 3.2 (Angriff auf die CAESAR-Verschlüsselung)

Wir vermuten, dass IEPPSKYD CAESAR-verschlüsselt ist. Wir verschieben die Buchstaben jeweils um eine Stelle weiter und betrachten das Ergebnis, bis ein sinnvoller Text entsteht:

IEPPSKYD -> JFQQTLZE -> KGRRUMAF -> LHSSVNBG -> MITTWOCH

Vermutlich war der Klartext also MITTWOCH verschlüsselt mit einer CAESAR-22-Verschlüsselung.

Bemerkung 3.2 (Lösungshinweise als CAESAR-Chiffretext)

Hinweise für Übungsaufgaben, die in Großbuchstaben geschrieben sind, werden wir meist CAESAR-13-verschlüsseln. Man kann dann eine Aufgabe zunächst ohne Hinweis versuchen zu lösen.

Bei der CAESAR-Chiffrierung werden die einzelnen Zeichen einer Zeichenkette mit einer Funktion \(f_K:\Sigma\to \Sigma\) (wie oben) verschlüsselt. Die Funktionen \(f_K\) sind dabei bijektive Abbildung zwischen dem Klartextraum \(\mathcal{P} = \Sigma^*\) und dem Chiffretextraum \(\mathcal{C} = \Sigma^*\). Somit können wir die CAESAR-Verschlüsselung also als spezielle Permutation des Alphabets \(\Sigma\) interpretieren, bei denen nur Verschiebungen um \(k \in \lbrace 1,\ldots,25\rbrace\) erlaubt sind.

3.1.2. MASC-Verschlüsselung

Wir haben in CAESAR-Verschlüsselung gesehen, dass die CAESAR-Verschlüsselung einen sehr kleinen Schlüsselraum der Mächtigkeit \(|\mathcal{K}| = |\Sigma|\) besitzt, wobei \(\Sigma\) das zu Grunde liegende Alphabet darstellt. Dies macht die Kryptoanalyse für dieses Verfahren trivial, da man nur alle möglichen Schlüssel testen und den potentiellen Klartext prüfen muss.

Um dieses Problem zu lösen wollen wir also eine Substitutionschiffre einführen, die einen wesentlich größeren Schlüsselraum als die CAESAR-Verschlüsselung besitzt. Daher diskutieren wir in diesem Abschnitt die sogenannte monoalphabetische Substitutionschiffrierung (kurz: MASC). Die grundlegende Idee ist es hierbei die CAESAR-Chiffrierung zu verallgemeinern, indem wir für die Funktionen \(f_k:\Sigma\to\Sigma\) beliebige Permutationen des Alphabets \(\Sigma\) zulassen.

Wir beschreiben im Folgenden eine praktikable Version der MASC-Chiffrierung für das aus den 26 Großbuchstaben bestehende Alphabet.

Algorithmus 3.2 (MASC-Verschlüsselung)

1. Wir wählen als zu Grunde liegendes Alphabet \(\Sigma\) die lateinischen Großbuchstaben (ohne deutsche Umlaute) A,…,Z und nutzen als Klartext- und Chiffretextraum \(\mathcal{P} = \mathcal{C} = \Sigma^*\), d.h. die Menge aller Wörter über dem Alphabet \(\Sigma\).

2. Schlüsselraum: Der Schlüssel wird durch ein Wort \(K \in \Sigma^*\) gegeben, also eine Zeichenfolge \(K=k_1k_2k_3\dots k_n\) mit Zeichen \(k_i \in \Sigma\) für \(i=1,\ldots,n\). Wir testen für \(i=1,\dots,n\), ob der Buchstabe \(k_i\) an einer späteren Stelle \(j>i\) im Wort nochmal vorkommt, d.h. ob \(k_i=k_j\) gilt. Falls ja, wird das Zeichen \(k_j\) an der späteren Stelle \(j\) herausgestrichen. Das (eventuell abgeänderte) Wort \(K\) besteht danach aus paarweise verschiedenen Buchstaben.

   An das Schlüsselwort \(K\) wird nun das (zyklisch permutierte) Alphabet angehängt, wobei mit dem nach \(k_n\) folgenden Buchstaben begonnen wird und alle Buchstaben weggelassen werden, die schon im gekürzten Schlüsselwort \(K\) vorkamen. Es bleibt schließlich ein Wort \(K = k_1k_2\dots k_{26} \in \Sigma^{26}\) mit 26 verschiedenen Buchstaben übrig, welches eindeutig eine Bijektion des Alphabets \(\Sigma\) induziert.

3. Verschlüsselung: Die bijektive Verschlüsselungsabbildung \(f_K:\{\text{A,B,C,\dots,Z}\}\to \{\text{A,B,C,\dots,Z}\}\) wird explizit durch \(f_K(\text{A})=k_1\), \(f_K(\text{B})=k_2\), \(f_K(\text{C})=k_3, \ldots, f_K(\text{Z})=k_{26}\) definiert und kann kompakt mit folgender Tabelle angegeben werden:

   \(x\)	A	B	C	…	Z
   \(f_K(x)\)	\(k_1\)	\(k_2\)	\(k_3\)	…	\(k_{26}\)

   Das bedeutet, dass man einfach das erweiterte Schlüsselwort \(k_1k_2k_3\dots k_{26} \in \Sigma^{26}\) unter das Alphabet schreibt. Auf den zu verschlüsselnden Klartext \(m = a_1a_2a_3\ldots \in \mathcal{P}\) wendet man dann zeichenweise die Verschlüsselungsfunktion \(f_K\) an und erhält so den Chiffretext

   \[c = f_K(a_1)f_K(a_2)f_K(a_3)\dots\]

4. Entschlüsselung: Da es sich bei der Verschlüsselungsabbildung \(f_K\) um eine Bijektion handelt liest man die entsprechende Tabelle von unten nach oben und erhält so die inverse Funktion \(f_K^{-1}\) für die Entschlüsselung. Auf den Chiffretext \(c = b_1b_2b_3\dots \in \mathcal{C}\) wendet man zeichenweise die Entschlüsselungsfunktion \(f_K^{-1}\) an und erhält somit den Klartext \(m = a_1a_2a_3\ldots \in \mathcal{P}\) durch:

   \[f_K(b_1)f_K(b_2)f_K(b_3)\dots \: = \: a_1a_2a_3\dots\]

Wir betrachten zunächst ein einfaches Beispiel für die MASC-Verschlüsselung eines Klartexts.

Beispiel 3.3 (MASC-Verschlüsselung)

Das Schlüsselwort ERLANGEN wird zuerst zu ERLANG verkürzt, dann zu ERLANGHIJKMOPQSTUVWXYZBCDF ergänzt. Dies liefert dann die folgende Bijektion \(f_k\):

\(x\)

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

\(f_k(x)\)

E

R

L

A

N

G

H

I

J

K

M

O

P

Q

S

T

U

V

W

X

Y

Z

B

C

D

F

Damit wird der Klartext HEUTE IST FREITAG zum Chiffretext INYXN JWX GVNJXEH verschlüsselt.

Bisher haben wir für Klartext und Geheimtext immer das gleiche Alphabet benutzt. Das muss im Allgemeinen in der Kryptographie jedoch nicht der Fall sein. Wir sprechen bei verschiedenen Alphabeten für den Klartext und den Chiffretext entsprechend vom Klartextalphabet und dem Geheimtextalphabet. Das folgende Beispiel nutzt ein unterschiedliches Klartext- und Geheimtextalphabet.

Beispiel 3.4 (MASC-Verschlüsselung mit unterschiedlichen Alphabeten)

Das Klartextalphabet \(\Sigma_1=\{\text{A,\dots,Z}\}\) bestehe aus den Zeichen mit ASCII-Werten zwischen 65 und 90, während das Geheimtextalphabet \(\Sigma_2=\{\text{',\dots,@}\}\) aus den Zeichen mit den ASCII-Werten zwischen 39 und 64 bestehe. Die Verschlüsselungsabbildung werde dann für die ASCII-Werte durch die mathematische Abbildung \(f(x)=x-26\) definiert, also

\(x\)

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

\(f(x)\)

‚

(

)

*

,

.

/

0

1

2

3

4

5

6

7

8

9

:

;

\(<\)

=

\(>\)

?

@

Aus dem Klartext DEPARTMENT MATHEMATIK wird dann der Chiffretext *+6’8:3+4: 3’:.+3’:/1.

Wie der (abgekürzte) Name MASC schon verrät handelt es sich bei Algorithmus 3.2 um ein monoalphabetisches Kryptosystem. Dies bedeutet, dass für die Verschlüsselung nur ein einziges (fest gewähltes) Geheimalphabet für die Verschlüsselung jedes Zeichens des Klartexts genutzt wird. Wir werden später noch sogenannte polyalphabetische Substitutionschiffren kennenlernen, die ein anderes Prinzip verfolgen und mehrere Geheimtextalphabete für die Verschlüsselung nutzen.

Beispiel 3.5 (MASC-Entschlüsselung)

In der Erzählung *The Gold-Bug * von Edgar Allan Poe kommt folgender Chiffretext vor:

53|\ddag\ddag\dag|305))6*;4826)4|\ddag|.)4|\ddag|);806*;48|\dag|8|\P|60))85;1|\ddag|(;:|\ddag|*8|\dag|83(88)
5*|\dag|;46(;88*96*?;8)*|\ddag|(;485);5*|\dag|2:*|\ddag|(;4956*2(5*-4)8|\P|8*;40692
85);)6|\dag|8)4|\ddag\ddag|;1(|\ddag|9;48081;8:8|\ddag|1;48|\dag|85;4)485|\dag|528806*81(|\ddag|9;48;(8
8;4(|\ddag|?34;48)4|\ddag|;161;:188;|\ddag|?;

Es handelt sich um eine monoalphabetische Substitutionschiffrierung (MASC), wobei aber das Klartextalphabet nicht mit dem Geheimtextalphabet übereinstimmt. Die zugehörige Verschlüsselungsabbildung \(f_K\) ergibt sich aus folgender Tabelle:

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

5

2

8

1

3

4

6

0

9

*

.

(

)

;

?

¶

:

Wendet man die entsprechende Entschlüsselungsfunktion \(f_K^{-1}\) an, so erhält man:

AGOODGLASSINTHEBISHOPSHOSTELINTHEDEVILSSEATFORTYONEDEGREESANDTHIRTEEN
MINUTESNORTHEASTANDBYNORTHMAINBRANCHSEVENTHLIMBEASTSIDESHOOTFROMTHE
LEFTEYEOFTHEDEATHSHEADABEELINEFROMTHETREETHROUGHTHESHOTFIFTYFEETOUT

In der Erzählung von Poe wird der Chiffretext auch systematisch entschlüsselt und das Ergebnis angegeben:

A GOOD GLASS IN THE BISHOP'S HOSTEL IN THE DEVIL'S SEAT - FORTY-ONE
DEGREES AND THIRTEEN MINUTES - NORTHEAST AND BY NORTH - MAIN BRANCH
SEVENTH LIMB EAST SIDE - SHOOT FROM THE LEFT EYE OF THE DEATH'S HEAD 
- A BEELINE FROM THE TREE THROUGH THE SHOT FIFTY FEET OUT.

Im Folgenden wollen wir einige Beobachtungen zur Sicherheit des MASC-Kryptosystems festhalten.

Bemerkung 3.3 (Kryptoanalyse für MASC-Verschlüsselung)

1. Die CAESAR-Verschlüsselung ist ein Spezialfall der MASC-Chiffrierung, indem man als Schlüsselwort nur einen einzelnen Großbuchstaben wählt. Der ergänzte Schlüssel ist dann durch die Vorgaben in Algorithmus 3.2 ein zyklisch permutiertes Alphabet.

2. Durch die Vorgabe eines erweiterten Schlüsselsworts \(K \in \Sigma^{26}\) mit paarweise verschiedenen Zeichen, lassen sich alle möglichen Permutation des zu Grunde liegenden Alphabets aus 26 Großbuchstaben realisieren. Damit ist die Größe des Schlüsselraums \(\mathcal{K}\) wesentlich größer als beim CAESAR-Verschlüsselungsverfahren. Wegen der kombinatorischen Möglichkeiten der möglichen Permutationen von 26 Buchstaben ergibt sich nämlich

   \[|\mathcal{K}| = 26! = 403291461126605635584000000 \approx 0.4\cdot 10^{27}\]

3. Trotz des wesentlich größeren Schlüsselraums kann eine MASC-Verschlüsselung insbesondere für längere Chiffretexte relativ zuverlässig geknackt werden. Hierbei verwendet man statistische Verfahren wie z.B. eine Häufigkeitsanalyse, welche wir in Häufigkeitsanalyse disktutieren wollen.

3.1.3. Häufigkeitsanalyse

Eine gängige Methoden um monoalphabetische Substitutionschiffren (wie die CAESAR- und die MASC-Verschlüsselung) zu brechen ist mit Hilfe einer statistischen Analyse der vorkommenden Zeichen im Geheimtextalphabet. Bei der sogenannten Häufigkeitsanalyse zählt man in einem vorgegebenen Chiffretext, wie häufig einzelne Zeichen einzelne Zeichen vorkommen.

Wenden wir die Häufigkeitsanalyse an einem realistischen Beispieltext an, so ergeben sich statistisch relevante Beobachtungen.

Beispiel 3.6 (Häufigkeitsanalyse eines deutschen Texts)

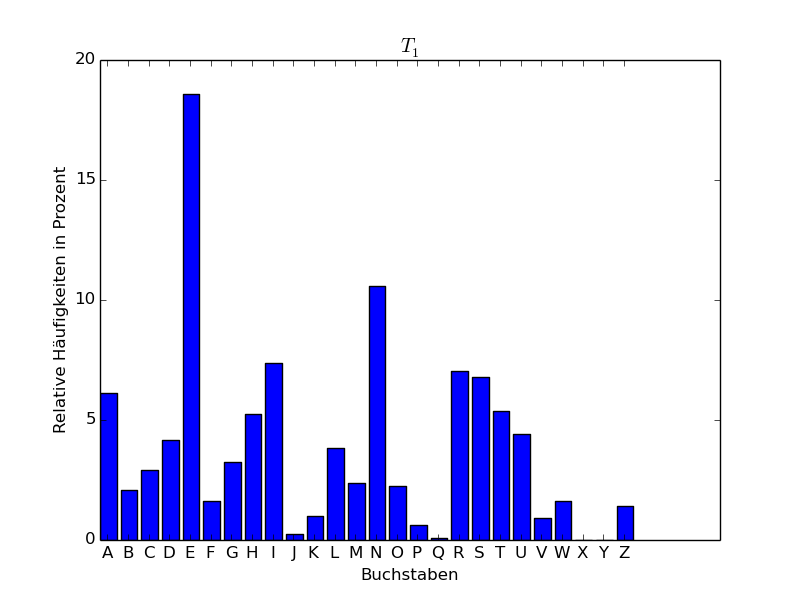
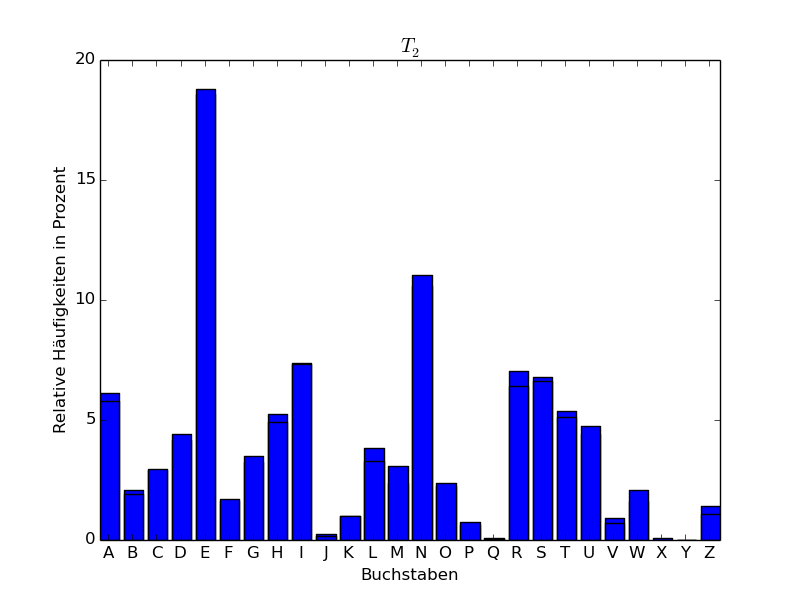
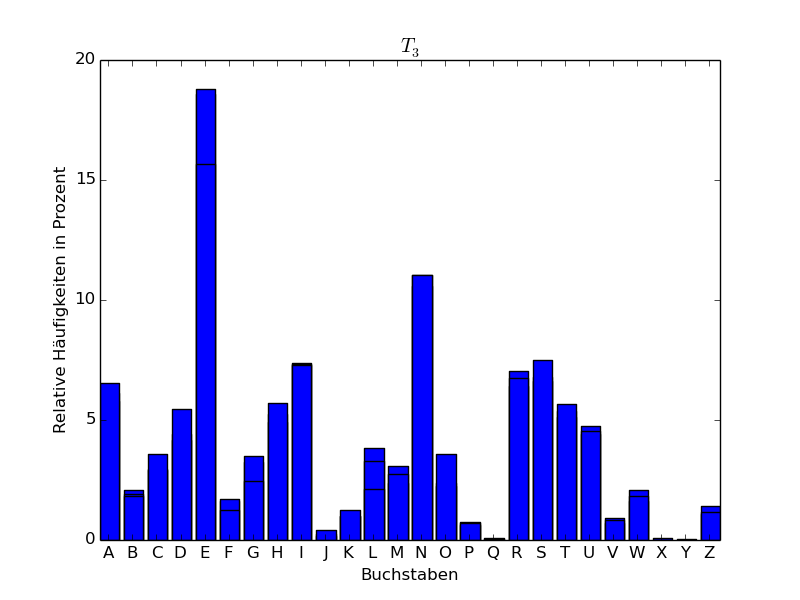
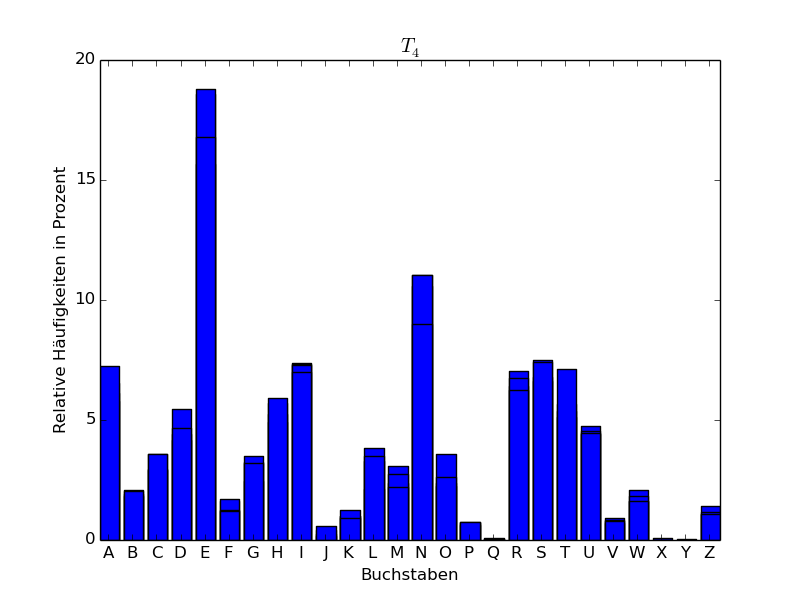
Wir haben den Abschnitt Ankunft  des ersten Kapitels von *Der Zauberberg * von Thomas Mann hergenommen, Umlaute umgewandelt (ä in ae, ö in oe, ü in ue, ß in ss), dann alles in lateinische Großbuchstaben umgewandelt und die Sonderzeichen weggelassen. Es blieben dann insgesamt 15442 Großbuchstaben übrig, was eine genügend große Stichprobe für eine statistische Analyse darstellt. Wir haben den resultierenden Text in 5 Teile \(T_1,\dots,T_5\) aufgeteilt zu 3000, 3000, 3000, 3000 und 3442 Zeichen und für die einzelnen sowie für den gesamten Abschnitt die relativen Häufigkeiten der einzelnen Buchstaben (d.h. der Monogramme des Texts) bestimmt. Das Ergebnis findet sich in folgender Tabelle, wobei die Zahlen in Prozent angegeben sind:

	\(T_1\)	\(T_2\)	\(T_3\)	\(T_4\)	\(T_5\)	gesamt
A	6.13	5.80	6.53	7.23	6.07	6.35
B	2.07	1.93	1.83	2.03	1.92	1.96
C	2.93	2.97	3.60	3.60	3.63	3.35
D	4.17	4.43	5.47	4.67	4.79	4.71
E	18.60	18.80	15.67	16.80	16.56	17.26
F	1.63	1.70	1.23	1.20	1.54	1.46
G	3.27	3.50	2.47	3.20	2.73	3.02
H	5.27	4.93	5.70	5.90	5.98	5.57
I	7.37	7.33	7.30	7.00	8.11	7.44
J	0.23	0.17	0.43	0.57	0.49	0.38
K	1.00	1.00	1.27	0.93	1.02	1.04
L	3.83	3.30	2.13	3.50	3.11	3.17
M	2.37	3.07	2.77	2.20	2.59	2.60
N	10.57	11.03	11.03	9.00	9.33	10.17
O	2.23	2.37	3.57	2.63	3.14	2.80
P	0.63	0.73	0.70	0.73	0.73	0.71
Q	0.07	0.03	0.00	0.03	0.00	0.03
R	7.03	6.40	6.73	6.23	6.80	6.64
S	6.80	6.63	7.50	7.43	7.93	7.28
T	5.37	5.13	5.67	7.13	6.30	5.93
U	4.43	4.77	4.53	4.47	3.95	4.42
V	0.93	0.70	0.83	0.80	0.46	0.74
W	1.63	2.10	1.83	1.63	1.51	1.74
X	0.00	0.10	0.00	0.00	0.00	0.02
Y	0.00	0.00	0.03	0.00	0.12	0.03
Z	1.43	1.07	1.17	1.07	1.19	1.19

Wenn wir die Buchstaben der Häufigkeit nach ordnen, erhalten wir für die Teile \(T_1,\dots,T_5\) folgende Tabelle:

\(T_1\)

E

N

I

R

S

A

T

H

U

D

L

G

C

M

O

B

F

W

Z

K

V

P

J

Q

X

Y

\(T_2\)

E

N

I

S

R

A

T

H

U

D

G

L

M

C

O

W

B

F

Z

K

P

V

J

X

Q

Y

\(T_3\)

E

N

S

I

R

A

H

T

D

U

C

O

M

G

L

B

W

K

F

Z

V

P

J

Y

Q

X

\(T_4\)

E

N

S

A

T

I

R

H

D

U

C

L

G

O

M

B

W

F

Z

K

V

P

J

Q

X

Y

\(T_5\)

E

N

I

S

R

T

A

H

D

U

C

O

L

G

M

B

F

W

Z

K

P

J

V

Y

Q

X

Man sieht also, dass E der häufigste Buchstabe ist. Mit einigem Abstand folgt dann der Buchstabe N.

Im Folgenden stellen wir die Häufigkeitsverteilungen auch graphisch in Form eines sogenannten Häufigkeitsgebirges dar.

{width=“48%“} {width=“48%“}

{width=“48%“} {width=“48%“}

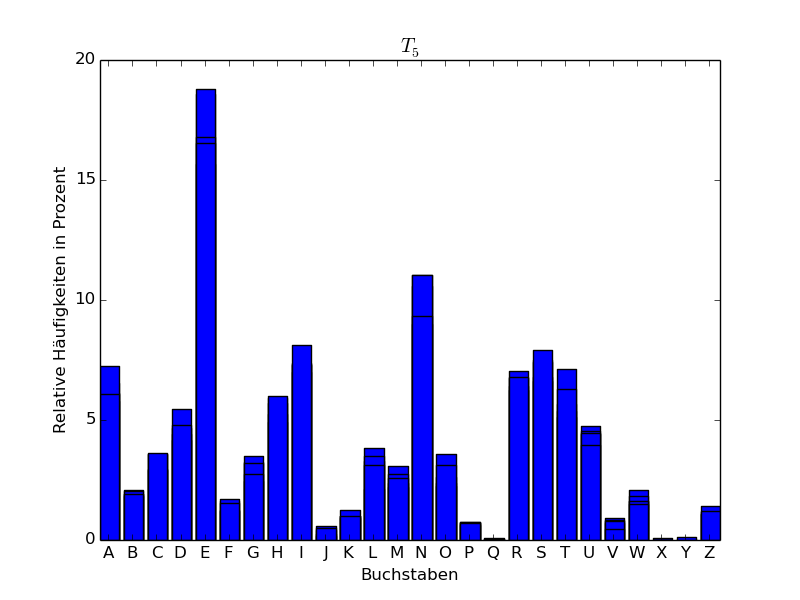{width=“48%“} 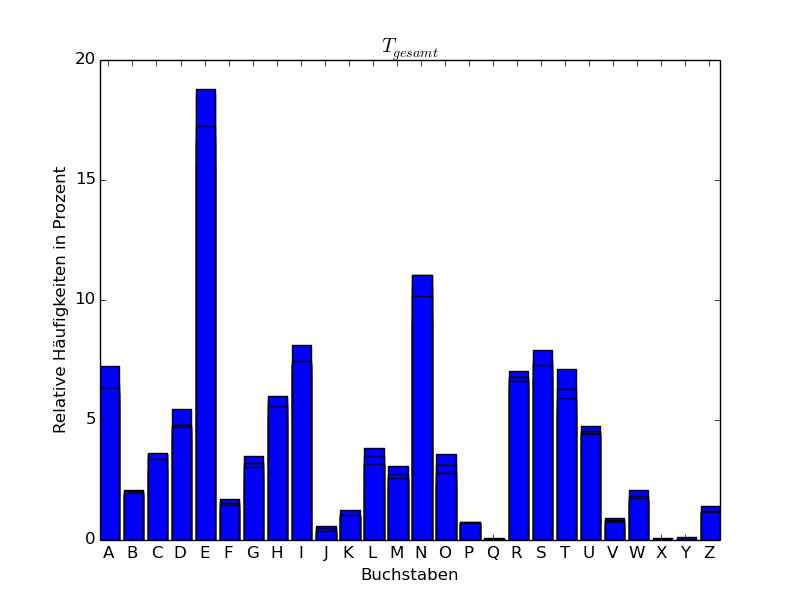{width=“48%“}

Auch bei Auswertung anderer deutscher Texte beobachtet man, dass E und dann N die häufigsten Buchstaben sind [Bau00]. Bei [Bau00] findet sich auch folgende Tabelle mit hypothetischen Zeichenwahrscheinlichkeiten  der englischen und deutschen Sprache, die durch Auswertung längerer Texte erstellt wurde:

Zeichen	englisch	deutsch	Zeichen	englisch	deutsch
A	8.04	6.47	N	7.09	9.84
B	1.54	1.93	O	7.60	2.98
C	3.06	2.68	P	2.00	0.96
D	3.99	4.83	Q	0.11	0.02
E	12.51	17.48	R	6.12	7.54
F	2.30	1.65	S	6.54	6.83
G	1.96	3.06	T	9.25	6.13
H	5.49	4.23	U	2.71	4.17
I	7.26	7.73	V	0.99	0.94
J	0.16	0.27	W	1.92	1.48
K	0.67	1.46	X	0.19	0.04
L	4.14	3.49	Y	1.73	0.08
M	2.53	2.58	Z	0.09	1.14

Natürlich kann man nicht erwarten, dass sich jeder einzelne Text an eine solche Verteilung hält. Jedoch liefert diese Tabelle gute Annäherungswerte zum Brechen von monoalphabetischen Substitutionschiffren.

Vermutet man, dass ein deutscher Text durch eine Substitutionschiffre verschlüsselt ist, wie zum Beispiel mit Hilfe der CAESAR-Chiffre, so bestimmt man das häufigste Zeichen \(b \in \Sigma\) des Chiffretexts und anschließend die Translation \(k \in \lbrace 0,\ldots,25\rbrace\), so dass \(f_k(\texttt{E})=b\) gilt. Anschließend testet man, ob sich durch Anwendung von \(f_{-k}\) auf den gesamten Chiffretext ein sinnvoller Text ergibt. Dieses Vorgehen wird in folgendem Beispiel illustriert.

Beispiel 3.7 (Häufigkeitsanalyse für CAESAR-Verschlüsselung)

Wir vermuten, dass folgender Text Caesar-chiffriert ist:

RLQFNRBBWRLQCFJBBXUUNBKNMNDCNWMJBBRLQBXCAJDARPKRWNRWVJNALQNWJDBJUCNWIN
RCNWMJBTXVVCVRAWRLQCJDBMNVBRWW

Die häufigsten Buchstaben sind B und N, die jeweils 12-mal vorkommen. Es ist \(f_{23}(\text{E})=\text{B}\) und \(f_{9}(\text{E})=\text{N}\). Wendet man zunächst \(f_{-23}\) auf den Chiffretext an, erhält man die (nicht recht sinnvolle) Zeichenfolge

UOTIQUEEZUOTFIMEEAXXQENQPQGFQZPMEEUOTEAFDMGDUSNUZQUZYMQDOTQZMGEMXFQZLQ
UFQZPMEWAYYFYUDZUOTFMGEPQYEUZZ

Wendet man hingegen die Entschlüsselungsfunktion \(f_{-9}\) an, so erhält man die sinnvolle Buchstabenfolge

ICHWEISSNICHTWASSOLLESBEDEUTENDASSICHSOTRAURIGBINEINMAERCHENAUSALTENZE
ITENDASKOMMTMIRNICHTAUSDEMSINN

Es handelt sich um die ersten Zeilen des Gedichts Die Loreley von Heinrich Heine.

Wir haben bisher nur die Verteilung von Großbuchstaben betrachtet. Werden auch andere Zeichen, wie zum Beispiel Sonder- und Interpunktionszeichen, verschlüsselt, sollte man auch hier Häufigkeitsverteilungen studieren. Wir betrachten auch hierzu im Folgenden ein Beispiel.

Beispiel 3.8 (Häufigkeitsanalyse für TeX-Dateien)

Wir haben 4 TeX-Dateien betrachtet und die vorkommenden Zeichen gezählt. Die Häufigkeit ist jeweils in Prozent angegeben. Wir haben nur die 10 häufigsten Zeichen aufgelistet, wobei (Nr. 32) als ASCII-Zeichen für Leerzeichen und (Nr. 10) für Return/Wagenrücklauf steht.

Datei
198407 Bytes
(Nr. 32)	12.52
e	4.81
n	3.02
1	2.83
i	2.77
0	2.49
(Nr. 10)	2.39
2	2.35
3	2.21
9	2.18

Datei
117364 Bytes
(Nr. 32)	8.19
\(\backslash\)	6.31
e	5.60
a	5.32
i	4.93
n	3.71
$	3.50
t	3.42
r	3.29
{	2.86

Datei
96471 Bytes
(Nr. 32)	13.59
e	3.24
1	3.13
0	3.06
A	2.66
4	2.64
9	2.59
3	2.53
8	2.44
D	2.40

Datei
74909 Bytes
(Nr. 32)	10.53
e	7.12
i	5.41
n	5.12
\(\backslash\)	4.23
a	3.83
$	3.65
t	3.50
r	3.10
(Nr. 10)	2.77

Mit Abstand ist also das Leerzeichen das häufigste verwendete Zeichen in diesen Dateien.

Neben der Häufigkeitsverteilung einzelner Zeichen ist auch die Häufigkeitsverteilung von Buchstabenkombinationen, also von sogenannten \(n\)-Grammen interessant.

Definition 3.1 (n-Gramme)

Sei \(\Sigma\) ein gewähltes Alphabet und \(n\in \N\). Wir bezeichnen ein Wort \(w = w_1w_2\ldots w_n \in \Sigma^n\) der Länge \(|w| = n\) über dem Alphabet \(\Sigma\) als \(\mathbf{n}\)-Gramm.

Für \(n=1\) spricht man von einem Monogramm, für \(n=2\) von einem Bigramm (oder auch Digramm, für \(n=3\) von einem Trigramm, usw.

Wir wollen die Häufigkeitsanalyse für Buchstabenkombinationen in folgendem Beispiel kurz erklären.

Beispiel 3.9 (Häufigkeitsanalyse für Bigramme)

Wir betrachten wieder den zuvor verwendeteten Text von Thomas Mann in Beispiel 3.6. Die folgenden Bigramme kommen mit einer Häufigkeit von mehr als einem Prozent vor:

EN	ER	CH	TE	ND	EI	IN	DE	GE	IE	ES	UN	NE	IC	SE	ST	BE
3.82	3.62	2.99	2.17	2.14	1.94	1.85	1.78	1.60	1.51	1.45	1.42	1.26	1.24	1.24	1.22	1.15

Dies sind die häufigsten Trigramme:

ICH	EIN	UND	SCH	DER	NDE	INE	END	CHT	GEN	CHE	ENS	TEN	TER	DIE	ERS
1.20	1.04	0.82	0.81	0.78	0.67	0.60	0.59	0.56	0.55	0.54	0.49	0.48	0.47	0.45	0.40

Die 10 häufigsten \(4\)-Gramme (Tetragramme) sind gezählt in absoluten Häufigkeiten:

EINE (83), ICHT (61), SICH (52), SEIN (48), NICH (45),
LICH (44), NDER (42), CHEN (40), SCHE (36), ENDE (36)

Bei [Bau00] findet sich eine Liste von häufigen Bigrammen in der deutschen Sprache. Als die zehn häufigsten deutschen Wörter werden genannt:

die, der, und, den, am, in, zu, ist, dass, es.

Es werden darüber hinaus noch viele weitere sprachliche Eigenschaften zusammengestellt. Dies kann helfen, eine monoalphabetische Substitutionschiffrierung recht zuverlässig zu entschlüsseln.

3.1.4. Homophone Substitutionschiffrierung

Bisher haben wir uns mit relativ einfachen, monoalphabetischen Substitutionschiffren beschäftigt, deren Verschlüsselungsfunktionen injektive Abbildungen in der Art realisieren, dass ein Klartext \(m=a_1a_2a_3\dots\) blockweise zu einem Chiffretext \(c=f(a_1)f(a_2)f(a_3)\dots\) verschlüsselt wird, wie z.B. die CAESAR- oder MASC-Verschlüsselung. Solche Substitutionschiffren können in der Regel sehr leicht mittels Häufigkeitsanalyse (siehe Häufigkeitsanalyse) gebrochen werden. Die größte Schwachstelle solcher Kryptosysteme ist die relative Häufigkeitsverteilung einzelner Zeichen, die je nach zu Grunde liegender Sprache einem klaren Muster folgt.

Um diese Schwachstelle zu umgehen wurde die sogenannte homophone Substitutionschiffrierung (aus dem Griechischen: gleich klingend) entwickelt, bei der ein Klartextzeichen nun durch mehrere unterschiedliche Chiffretextzeichen ersetzt werden kann. Damit lassen sich die relativen Häufigkeiten einzelner Zeichen verschleiern und statistische Angriffsmethoden signifikant erschweren.

Algorithmus 3.3 (Homophone Substitutionschiffrierung)

1. Wir wählen als zu Grunde liegendes Klartextalphabet \(\Sigma_1\) die lateinischen Großbuchstaben (ohne deutsche Umlaute) A,…,Z und nutzen als Klartextraum \(\mathcal{P} = \Sigma_1^*\), d.h. die Menge aller Wörter über dem Alphabet \(\Sigma_1\).

2. Wir wählen als zu Grunde liegendes Geheimtextalphabet \(\Sigma_2\) die Menge der zweistelligen Dezimalzahlen 00, 01, …, 98, 99 und nutzen als Chiffretextraum \(\mathcal{C} = \Sigma_2^*\), d.h. die Menge aller Wörter über dem Alphabet \(\Sigma_2\).

3. Schlüsselraum: Für jedes Klartextzeichen \(a_i\in \Sigma_1\) wählt man eine Teilmenge des Geheimtextalphabets \(F(a_i)\subseteq \Sigma_2\), wobei die Mengen \(F(a_i)\) für verschiedene Klartextzeichen \(a_i \in \Sigma_1\) disjunkt sein sollen, d.h. es gilt

   \[F(a_i)\cap F(a_j) = \emptyset \text{ für } a_i\ne a_j.\]

   Die geheime Zuordnung zwischen Klartext- und Geheimtextzeichen lässt sich mittels einer \(10 \times 10\)-Tabelle festlegen. Der Schlüsselraum \(\mathcal{K}\) ist dann gegeben als die Menge aller möglichen Zuordnungstabellen \(k \in \mathcal{K}\).

4. Verschlüsselung: Ein Klartext \(m \in \mathcal{P}\) mit \(m = a_1a_2a_3\dots\) wird zu einem Chiffretext \(c \in \mathcal{C}\) mit \(c = b_1b_2b_3\dots\) verschlüsselt, indem für jedes Klartextzeichen \(a_i \in \Sigma_1\) zufällig ein Chiffretextzeichen \(b_i\in F(a_i)\) in der Tabelle ausgewählt wird.

5. Entschlüsselung: Ein Chiffretext \(c \in \mathcal{C}\) mit \(c = b_1b_2b_3\dots\) wird zu einem Klartext \(m \in \mathcal{P}\) mit \(m = a_1a_2a_3\dots\) entschlüsselt, indem für jedes Chiffretextzeichen \(b_i \in \Sigma_2\) das entsprechende Klartextzeichen \(a_i \in \Sigma_1\) aus der Tabelle verwendet wird.

Wir betrachten im Folgenden eine historische Zuordnungstabelle für eine homophone Substitutionschiffre.

Beispiel 3.10 (Verschlüsselung mit homophoner Substitution)

Ungefähr folgende Tabelle wurde im 2. Weltkrieg auf amerikanischer Seite von Brigadier General Leslie R. Groves benutzt []:

	1	2	3	4	5	6	7	8	9	0
1	I	P	I		O	U	O		P	N
2	W	E	U	T	E	K		L	O
3	E	U	G	N	B	T	N		S	T
4	T	A	Z	M	D		I	O	E
5	S	V	T	J		E		Y		H
6	N	A	O	L	N	S	U	G	O	E
7		C	B	A	F	R	S		I	R
8	I	C	W	Y	R	U	A	M
9	M	V	T		H	P	D	I	X	Q
0	L	S	R	E	T	D	E	A	H	E

Um einen Klartextbuchstaben zu verschlüsselt sucht man sich zufällig eine Stelle in der Tafel, wo dieser auftritt, und notiert sich dann Zeilen- und Spaltennummer als zweistellige Dezimalzahl. So würde der Klartext TODAY zu 24 69 06 42 58 oder auch zu 41 63 97 62 84 verschlüsselt werden.

Es stellt sich heraus, dass die Sicherheit der homophonen Substitutionschiffre maßgeblich von der getroffenen Wahl der Teilmengen an Geheimtextzeichen \(F(a) \subset \Sigma_2\) für ein Klartextzeichen \(a \in \Sigma_1\) abhängt. Dies wollen wir im Folgenden genauer analysieren.

Sei \(h(a) \geq 0\) die relative Häufigkeit, mit der das Klartextzeichen \(a \in \Sigma_1\) in einem durchschnittlichen Text auftritt. Wählen wir bei der Verschlüsselung ein zugeordnetes Geheimtextzeichen \(b\in F(a)\) (gleichverteilt) zufällig, so wird die relative Häufigkeit \(h(b) \geq 0\) eines Geheimtextzeichens \(b\in F(a)\) im Chiffretext bestimmt sein durch

\[h(b) \ \approx \ \frac{h(a)}{|F(a)|}.\]

Wollen wir realisieren, dass alle Geheimtextzeichen im verschlüsselten Text gleichhäufig auftreten, so müssen wir verlangen, dass die relative Häufigkeit \(h(b)\) unabhängig vom gewählten Klartextzeichen \(a \in \Sigma_1\) ist. Dies bedeutet, dass die relative Häufigkeit aller Geheimtextzeichen \(b \in \Sigma_2\) konstant sein soll, d.h. \(h(b) = \frac{1}{c}\) für eine Konstante \(c \geq 1\), und somit gilt durch Umstellen

\[|F(a)|\approx c\cdot h(a)\quad\text{ für alle }\quad a\in\Sigma_1.\]

Ist \(N=\sum_{a\in\Sigma_1}|F(a)| \leq |\Sigma_2|\) die Anzahl der verwendeten Geheimtextzeichen, so gilt also

\[N \, = \, \sum_{a\in\Sigma_1}|F(a)| \ \approx \ \sum_{a\in \Sigma_1} c\cdot h(a) \ = \ c\cdot \underbrace{\sum_{a\in \Sigma_1}h(a)}_{=\,1} \, = \, c.\]

Das bedeutet, dass eine vernünftige Wahl der Konstante \(c \geq 1\) die Anzahl der verwendeten Geheimtextzeichen sein muss. Hieraus folgt, dass die Anzahl der zugeordneten Geheimtextzeichen für ein Klartextzeichen \(a \in \Sigma_1\) gewählt werden muss als:

\[|F(a)| \ \approx \ N \cdot h(a).\]

Bei dieser Wahl der zugeordneten Geheimtextzeichen \(F(a) \subset \Sigma_2\) treten die Geheimtextzeichen alle ungefähr gleich häufig auf. In diesem Fall erhält man durch eine einfache Häufigkeitsanalyse der Zeichen keine zusätzlichen Informationen. Eine Möglichkeit Muster in homophonen Substitutionen zu erkennen ist es dann nach Buchstabenkombinationen, d.h. nach Bigrammen zu suchen. Beispielsweise folgt im Deutschen auf den Buchstaben Q immer ein U. Häufig kommen folgende Buchstabenpaare in deutschen Wörtern vor:

ER, EN, CH, DE, EI, ND, TE, \dots

Beispiel 3.11 (Anzahl der zugeordneten Geheimtextzeichen)

Wir wählen in diesem Beispiel für die homophone Substitutionschiffre das Klartextalphabet \(\Sigma_1=\{\mathrm{A},\dots,\mathrm{Z}\}\) und das Geheimtextalphabet \(\Sigma_2=\{00,01,\dots,99\}\). In der folgenden Tabelle ist \(h(a)\) eine hypothetische relative Zeichenwahrscheinlichkeit (in \(\%\) angegeben) des Klartextzeichens \(a \in \Sigma_1\), wie sie sich bei [] findet. Dazu wählen wir \(F(a)\approx 100\cdot h(a)\), so dass für die Anzahl der zugeordneten Geheimtextzeichen \(|F(a)|\ge 1\) gilt, d.h. jedes Klartexteichen muss sich verschlüsseln lassen. Außerdem erfüllen wir die Nebenbedingung

\[\sum_{a\in \Sigma_1} |F(a)| \, = \, 100 \, = \, |\Sigma_2|\]

Das führt zu der folgenden Anzahl an zugeordneten Geheimtextzeichen \(|F(a)|\) für jedes Klartextzeichen \(a \in \Sigma_1\):

	\(h(a)\)	\(|F(a)|\)
A	6.47	6
B	1.93	2
C	2.68	* 2
D	4.83	5
E	17.48	17
F	1.65	2
G	3.06	3
H	4.23	4
I	7.73	8
J	0.27	* 1
K	1.46	1
L	3.49	3
M	2.58	* 2

	\(h(a)\)	\(|F(a)|\)
N	9.84	10
O	2.98	3
P	0.96	1
Q	0.02	* 1
R	7.54	* 7
S	6.83	7
T	6.13	6
U	4.17	4
V	0.94	1
W	1.48	1
X	0.04	* 1
Y	0.08	* 1
Z	1.14	1

Das Zeichen * in der dritten Spalte der obigen Tabelle bedeutet, dass \(|F(a)|\) nicht als die nächstgelegene ganze Zahl zu \(100\cdot h(a)\) gewählt wurde.

Eine mögliche Realisierung der Zuordnungstabelle für die homophone Substitutionschiffre mit den vorigen Überlegungen ist:

\(a\)	\(F(a)\)
A	\(\{11,20,30,68,77,85\}\)
B	\(\{91,94\}\)
C	\(\{10,39\}\)
D	\(\{02,08,41,51,93\}\)
E	\(\{04,07,17,18,22,32,35,44,49,53,56,57,60,64,73,74,90\}\)
F	\(\{24,36\}\)
G	\(\{09,25,65\}\)
H	\(\{14,40,47,66\}\)
I	\(\{03,12,15,43,76,95,97,98\}\)
J	\(\{42\}\)
K	\(\{27\}\)
L	\(\{79,81,92\}\)
M	\(\{88,89\}\)
N	\(\{05,06,19,38,54,58,59,61,69,83\}\)
O	\(\{16,55,84\}\)
P	\(\{71\}\)
Q	\(\{34\}\)
R	\(\{00,01,23,28,37,46,48\}\)
S	\(\{21,29,52,63,67,86,87\}\)
T	\(\{26,33,70,72,75,82\}\)
U	\(\{45,62,96,99\}\)
V	\(\{80\}\)
W	\(\{78\}\)
X	\(\{50\}\)
Y	\(\{13\}\)
Z	\(\{31\}\)

Damit verschlüsselt sich der Klartext KRYPTOGRAPHIEUNDMATHEMATIK zu

27 01 13 71 26 55 25 46 85 71 47 43 90 96 05 02 89 30 26 40 73 89 85 33 95 27 

oder auch zu

27 37 13 71 82 55 25 23 68 71 47 43 18 99 38 08 88 11 75 14 07 88 68 72 97 27 

3.1.5. ALBC-Verschlüsselung

In diesem Abschnitt wollen wir uns mit einer monoalphabetischen Substitutionschiffre beschäftigen, die nicht auf Monogrammen operiert, sondern mit Blocklänge \(L=2\), d.h. auf Bigrammen operiert. Der Name ALBC-\(2\) leitet sich aus dem zu Grunde liegenden Prinzip einer affin-linearen Transformation von Blöcken ab.

Algorithmus 3.4 (ALBC-2-Verschlüsselung:)

1. Wir wählen als zu Grunde liegendes Alphabet \(\Sigma\) die lateinischen Großbuchstaben (ohne deutsche Umlaute) A,…,Z und nutzen als Klartext- und Chiffretextraum \(\mathcal{P} = \mathcal{C} = \Sigma^*\), d.h. die Menge aller Wörter über dem Alphabet \(\Sigma\).

2. Schlüsselraum: Ein Schlüssel \(k \in \mathcal{K}\) ist ein \(6\)-Tupel

   \[k=(k_1,k_2,k_3,k_4,k_5,k_6)\text{ mit }0\le k_i\le 25 \quad \text{ und } \quad \ggT(k_1k_5-k_2k_4,26)=1.\]

   Die zugehörige Verschlüsselungsabbildung \(f_k \in \mathcal{E}\) operiert auf Blöcken der Länge \(2\) wie folgt:

   \[f_k(x,y)=(k_1x+k_2y+k_3\bmod 26,k_4x+k_5y+k_6\bmod 26).\]

   Identifizieren wir ein Bigramm \((x,y)\) mittels der kanonischen Bijektion mit dem Vektor \((x,y)^T \in \{0,\ldots,25\} \times \{0,\ldots,25\}\), so können wir die Verschlüsselungsabbildung \(f_k\) auch in Matrixschreibweise schreiben als

   \[f_{k}\left[\left(\begin{array}{cc}x\\y\end{array}\right)\right] \ = \ \left(\begin{array}{cc}k_1&k_2\\k_4&k_5\end{array}\right) \left(\begin{array}{c}x\\y\end{array}\right)+ \left(\begin{array}{c}k_3\\k_6\end{array}\right)\bmod 26.\]

   Die Modulo-Arithmetik ist hierbei komponentenweise zu verstehen.

   Die Bedingung der Teilerfremdheit \(\ggT(k_1k_5-k_2k_4,26)=1\) impliziert, dass eine ganze Zahl \(d\in \Z\) existiert mit

   \[d \cdot (k_1k_5-k_2k_4)\bmod 26=1,\]

   welche beispielsweise durch Ausprobieren gefunden werden kann.

   Definiert man dann

   \[\begin{aligned} \ell_1 &=& d \cdot k_5 \bmod 26,\\ \ell_2 &=& (-d \cdot k_2)\bmod 26,\\ \ell_3 &=& d\cdot (k_2k_6-k_3k_5)\bmod 26,\\ \ell_4 &=& (-d \cdot k_4)\bmod 26,\\ \ell_5 &=& d \cdot k_1\bmod 26,\\ \ell_6 &=& d \cdot (k_3k_4-k_1k_6)\bmod 26, \end{aligned}\]

   so gilt für

   \[\ell \ := \ (\ell_1,\ell_2,\ell_3,\ell_4,\ell_5,\ell_6)\]

   die Beziehung \(f_k^{-1}=f_{\ell} \in \mathcal{D}\). Das so berechnete 6-Tupel \(\ell \in \mathcal{K}\) ist der zu \(k \in \mathcal{K}\) inverse Schlüssel.

3. Verschlüsselung: Der Ausgangstext \(m \in \mathcal{P}\) wird zunächst in Blöcke der Länge \(k=2\) unterteilt, wobei am Schluss eventuell ein beliebiges Zeichen zu ergänzen ist, falls die Anzahl der Buchstaben im Klartext ungerade ist. Der Text wird also indiziert als \(m = x_1y_1x_2y_2x_3y_3\dots\). Mit

   \[\tilde{x}_i \ := \ k_1x_i+k_2y_i+k_3\bmod N \quad \text{ und } \quad \tilde{y}_i \ := \ k_4x_i+k_5y_i+k_6\bmod N\]

   wird der Chiffretext \(c \in \mathcal{C}\) zu \(c = \tilde{x}_1 \tilde{y}_1 \tilde{x}_2 \tilde{y}_2 \tilde{x}_3 \tilde{y}_3\dots\)

4. Entschlüsselung: Die Entschlüsselung funktioniert analog wie die Verschlüsselung, nur dass man statt des Schlüssels \(k=(k_1,\dots,k_6)\) den inversen Schlüssel \(\ell=(\ell_1,\dots,\ell_6)\) benutzt:

   \[x_i=\ell_1\tilde{x}_i+\ell_2\tilde{y}_i+\ell_3\bmod 26,\quad y_i=\ell_4\tilde{x}_i+\ell_5\tilde{y}_i+\ell_6\bmod 26.\]

Wir wollen die Funktionsweise des ALBC-2-Kryptosystems an Hand eines Beispiels für die Chiffrierung illustrieren.

Beispiel 3.12 (ALBC-2-Verschlüsselung)

Wir wählen den Schlüssel \(k=(5,8,17,23,15,14)\). Wir erkennen, dass dies ein zulässiger Schlüssel ist, da gilt

\[k_1k_5-k_2k_4 \ = \ 5\cdot 15-8\cdot 23 \ = \ -109 = -5\cdot 26+21,\]

und \(\ggT(-109,26) = 1\) ist, da \(109\) eine Primzahl ist. Durch Ausprobieren finden wir heraus, dass die ganze Zahl \(d=5\) die Bedingung \(d \cdot (k_1k_5-k_2k_4)\bmod 26=1\) erfüllt. Damit kann man direkt den inversen Schlüssel \(\ell \in \mathcal{K}\) berechnen als:

\[\begin{aligned} \ell_1 &=& dk_5 \bmod 26 = 75\bmod 26 = 23,\\ \ell_2 &=& (-dk_2)\bmod 26 = (-40) \bmod 26 = 12,\\ \ell_3 &=& d(k_2k_6-k_3k_5)\bmod 26 = (-715) \bmod 26 = 13,\\ \ell_4 &=& (-dk_4)\bmod 26 = (-115) \bmod 26 = 15,\\ \ell_5 &=& dk_1\bmod 26 = 25\bmod 26=25,\\ \ell_6 &=& d(k_3k_4-k_1k_6)\bmod 26 = 1605\bmod 26 = 19. \end{aligned}\]

Der inverse Schlüssel ist somit \(\ell=(23,12,13,15,25,19)\).

Wir wollen den Klartext ZAHLENTHEORIE verschlüsseln. Wir hängen den willkürlichen Buchstaben X an, damit die Zeichenzahl gerade ist, wandeln den Text in eine Zahlenfolge \(x_1y_1\dots x_7y_7\) um. Nun berechnen wir die affin-lineare Transformation als

\[\tilde{x}_i=k_1x_i+k_2y_i+k_3\bmod 26,\quad \tilde{y}_i=k_4x_i+k_5y_i+k_6\bmod 26\]

und wandeln die resultierende Zahlenfolge \(\tilde{x}_1\tilde{y}_1\dots \tilde{x}_7\tilde{y}_7\) wieder mittels der kanonische Bijektion in eine entsprechende Buchstabenfolge um:

ZA	\((12,17)\)	\((25,0)\)	MR
HL	\((10,2)\)	\((7,11)\)	KC
EN	\((11,15)\)	\((4,13)\)	LP
TH	\((12,10)\)	\((19,7)\)	MK
EO	\((19,4)\)	\((4,14)\)	TE
RI	\((10,5)\)	\((17,8)\)	KF
EX	\((13,9)\)	\((4,23)\)	NJ

Der durch die ALBC-2-Verschlüsselung erzeugte Chiffretext ist also

MRKCLPMKTEKFNJ

Bemerkung 3.4 (Eigenschaften der ALBC-Verschlüsselung)

1. Wenn wir später die Kongruenzrechnung ausführlich behandeln, werden wir sehen, woher genau die Bedingung der Teilerfremdheit kommt und wie sich der inverse Schlüssel aus dem Schlüssel berechnen lässt.

2. Natürlich verallgemeinert sich ALBC-\(2\) sofort auf Alphabete mit \(N \in \N\) Zeichen, wenn man die verwendete Modulo-Arithmetik anpasst.

3. Verwendet man ALBC-\(2\) mit einem \(N\)-elementigen Alphabet, das mittels der kanonischen Bijektion mit den Zahlen \(0,\dots,N-1\) identifiziert wird, so ist die Menge der Schlüssel

   \[\{(k_1,k_2,k_3,k_4,k_5,k_6): 0\le k_i\le N-1, \ggT(N,k_1k_5-k_2k_4)=1\}.\]

   Man kann zeigen, dass die Anzahl der Schlüssel sich berechnen lässt als

   \[N^6\prod_{p|N}(1-\frac{1}{p}) (1-\frac{1}{p^2})\]

   Für \(N=26\) ergibt sich somit eine Anzahl von \(|\mathcal{K}| = 106299648\) möglichen Schlüsseln.

Bemerkung 3.5 (Kryptoanalyse für die ALBC-2-Verschlüsselung)

Wir nehmen an, wir kennen den Chiffretext einer ALBC-\(2\)-Verschlüsselung, also \(\tilde{x}_1\tilde{y}_1\tilde{x}_2 \tilde{y}_2\dots\). Außerdem kennen wir oder raten wir Teile des Klartexts (also eine Known-plaintext Attacke), wie beispielsweise den Anfang \(x_1y_1x_2y_2x_3y_3\). Dann erhalten wir (mit obigen Bezeichnungen) das folgende Kongruenzgleichungssystem:

\[\begin{aligned} x_1\equiv \ell_1\tilde{x}_1+\ell_2\tilde{y}_1+\ell_3\bmod 26, && y_1\equiv \ell_4\tilde{x}_1+\ell_5\tilde{y}_1+\ell_6\bmod 26, \\ x_2\equiv \ell_1\tilde{x}_2+\ell_2\tilde{y}_2+\ell_3\bmod 26, && y_2\equiv \ell_4\tilde{x}_2+\ell_5\tilde{y}_2+\ell_6\bmod 26, \\ x_3\equiv \ell_1\tilde{x}_3+\ell_2\tilde{y}_3+\ell_3\bmod 26, && y_3\equiv \ell_4\tilde{x}_3+\ell_5\tilde{y}_3+\ell_6\bmod 26. \end{aligned}\]

Dies sind 6 Gleichungen mit 6 unbekannten Zahlen \(\ell_1,\dots,\ell_6\). Man kann hoffen, dass man diese Gleichungen lösen kann. Daher ist ALBC-\(2\) ziemlich unsicher. (Bei SAGE gibt es hierfür eine native Funktion solve_mod.)

Eine mathematisch naheliegende Verallgemeinerung des ALBC-\(2\)-Kryptosystems ist das folgende Verfahren, das wir nur kurz skizzieren. Dies ist eine direkte Erweiterung von Algorithmus 3.4 für eine beliebige Blocklänge \(L = k \in \N, k \geq 2\).

Algorithmus 3.5 (ALBC-k-Verschlüsselung)

Wir nehmen ein zu Grunde liegendes Alphabet mit \(N\) Zeichen an, das über die kanonische Bijektion mit den Zahlen zwischen \(0\) und \(N-1\) identifiziert wird. Nun fassen wir jeweils einen Block aus \(k\in\N, k\geq 2\) Zeichen \(x_1x_2\dots x_k\) zu einer Nachrichteneinheit zusammen. Hieraus bilden wir einen Vektor in \(\Z_N^k\) und definieren die Verschlüsselungsabbildung durch

\[\left(\begin{array}{c}x_1\\ \vdots\\ x_k\end{array}\right)\mapsto A \left(\begin{array}{c}x_1\\ \vdots\\ x_k\end{array}\right)+ \left(\begin{array}{c}b_1\\ \vdots\\ b_k\end{array}\right)\bmod N\]

mit einer ganzzahligen Matrix \(A \in \Z_N^{k \times k}\) und ganzen Zahlen \(b_1,\dots,b_k \in \Z_N\), so dass \(\ggT(\det A,N)=1\) ist. Die Teilerfremdheit von \(\det A\) und \(N\) sichert die Bijektivität der Verschlüsselungsabbildungen.

3.1.6. PLAYFAIR-Chiffre

In diesem Abschnitt beschäftigen wir uns mit einer Substitutionschiffre für Bigramme (d.h. für eine Blockgröße \(n=2\)), die Mitte des 19. Jahrhunderts von dem britischen Physiker Charles Wheatstone ausgedacht wurde und anschließend im ersten und zweiten Weltkrieg genutzt wurde. Die Grundidee dieser Verschlüsselung ist es ein 5x5-Raster entsprechend eines geheimen Kennworts zu erstellen und Paare von Klartextbuchstaben anhand ihrer zueinander relativen Position innerhalb des Rasters zu ersetzen.

Algorithmus 3.6 (PLAYFAIR-Verschlüsselung)

1. Wir wählen als zu Grunde liegendes Alphabet \(\Sigma\) die lateinischen Großbuchstaben (ohne deutsche Umlaute) A,…,Z ohne den Buchstaben J mit \(|\Sigma| = 25\). Kommt der Buchstabe J im Klartext vor, so ersetzen wir ihn durch den Buchstaben I. Wir nutzen als Klartext- und Chiffretextraum \(\mathcal{P} = \mathcal{C} = \Sigma^*\), d.h. die Menge aller Wörter über dem Alphabet \(\Sigma\).

2. Schlüsselraum: Wir schreiben zunächst ein geheimes Schlüsselwort \(k \in \mathcal{K}=\Sigma^*\) zeilenweise in eine \(5\times 5\)-Matrix \(M=(a_{i,j})_{1\le i,j\le 5}\), die auch PLAYFAIR-Quadrat genannt wird. Steht ein Buchstabe bereits in der Matrix, so überspringen wir ihn. Den Rest der Matrix füllen wir mit den restlichen Buchstaben des Alphabets \(\Sigma\) in alphabetischer Reihenfolge auf. Die Matrix enthält schließlich alle 25 von J verschiedenen Großbuchstaben.

   Beispielsweise liefert das Code-Wort KRYPTOGRAPHIE die Matrix

   K	R	Y	P	T
   O	G	A	H	I
   E	B	C	D	F
   L	M	N	Q	S
   U	V	W	X	Z

3. Verschlüsselung:

   1. Zuerst unterteilen wir den Klartext in Blöcke der Länge \(n=2\). Hierbei müssen wir eventuell den Buchstaben X anhängen, damit alle Klartextblöcke aus zwei verschiedenen Zeichen bestehen. Der Klartext WASSER wird also zu WA SX SE RX.

   2. Wir interpretieren nun jeden Klartextblock als \(a_{i_1,j_1} a_{i_2,j_2}\), d.h. das erste Zeichen des Blocks hat Zeilenindex \(i_1\) und Spaltenindex \(j_1\), das zweite entsprechend Zeilenindex \(i_2\) und Spaltenindex \(j_2\).

      Wir unterscheiden nun zwischen den folgenden drei Fällen:

      • Ist \(i_1=i_2\), d.h. die beiden Zeichen stehen in der gleichen Zeile, so wird der Block zu \(a_{i_1,j_1+1} a_{i_2,j_2+1}\) verschlüsselt, wobei die Indizes modulo \(5\) zu betrachten sind. Man rückt also die beiden Zeichen eine Spalte nach rechts (periodisch fortgesetzt).

      • Ist \(j_1=j_2\), d.h. die beiden Zeichen stehen in der gleichen Spalte, so wird der Block zu \(a_{i_1+1,j_1}a_{i_2+1,j_2}\) verschlüsselt, wobei die Indizes modulo \(5\) zu betrachten sind. Man rückt also die beiden Zeichen eine Zeile nach unten (periodisch fortgesetzt).

      • Ist \(i_1\ne i_2\) und \(j_1\ne j_2\), d.h. die beiden Zeichen stehen in unterschiedlichen Spalten und Zeilen, so wird der Block zu \(a_{i_1,j_2} a_{i_2,j_1}\) verschlüsselt. Man vertauscht also die jeweiligen Spalten der beiden Zeichen.

      Die Klartextblöcke WA SX SE RX werden mit dem obigen PLAYFAIR-Quadrat also zu YC QZ LF PV verschlüsselt.

4. Entschlüsselung:

   1. Wir erstellen aus dem geheimen Schlüsselwort \(k \in \mathcal{K}\) wie zuvor eine \(5\times 5\)-Matrix.

   2. Wir interpretieren nun jeden Klartextblock als \(a_{i_1,j_1} a_{i_2,j_2}\), d.h. das erste Zeichen des Blocks hat Zeilenindex \(i_1\) und Spaltenindex \(j_1\), das zweite entsprechend Zeilenindex \(i_2\) und Spaltenindex \(j_2\).

      Wir unterscheiden nun zwischen den folgenden drei Fällen:

      • Ist \(i_1=i_2\), d.h. die beiden Zeichen stehen in der gleichen Zeile, so wird der Block zu \(a_{i_1,j_1-1} a_{i_2,j_2-1}\) entschlüsselt, wobei die Indizes modulo \(5\) zu betrachten sind. Man rückt also die beiden Zeichen eine Spalte nach links (periodisch fortgesetzt).

      • Ist \(j_1=j_2\), d.h. die beiden Zeichen stehen in der gleichen Spalte, so wird der Block zu \(a_{i_1-1,j_1} a_{i_2-1,j_2}\) entschlüsselt, wobei die Indizes modulo \(5\) zu betrachten sind. Man rückt also die beiden Zeichen eine Zeile nach oben (periodisch fortgesetzt).

      • Ist \(i_1\ne i_2\) und \(j_1\ne j_2\), d.h. die beiden Zeichen stehen in unterschiedlichen Spalten und Zeilen,, so wird der Block zu \(a_{i_1,j_2} a_{i_2,j_1}\) entschlüsselt. Man vertauscht also die jeweiligen Spalten der beiden Zeichen.

Wir wollen die Funktionsweise des PLAYFAIR-Kryptosystems in folgendem Beispiel verdeutlichen.

Beispiel 3.13 (PLAYFAIR-Verschlüsselung)

Wir wollen den Klartext

DIE KLASSISCHE AUFGABE DER KRYPTOGRAPHIE IST ES EINE NACHRICHT ODER
AUFZEICHNUNG FÜR DEN UNBEFUGTEN UNVERSTAENDLICH ZU MACHEN

mit dem Passwort KRYPTOGRAPHIE Playfair-chiffrieren. Im ersten Schritt unterteilen wir den Text in Bigramme und fügen eventuell ein X ein:

DI EK LA SX SI SC HE AU FG AB ED ER KR YP TO GR AP HI EI ST ES EI NE NA CH RI CH TO 
DE RA UF ZE IC HN UN GF UE RD EN UN BE FU GT EN UN VE RS TA EN DL IC HZ UM AC HE NX

Mit dem Playfair-Quadrat aus Algorithmus 3.6 (zum Passwort KRYPTOGRAPHIE) erhalten wir so den folgenden Chiffretext:

FH LO NO QZ ZF NF OD OW BI GC BF BK RY PT KI BG HY IO FO ZI FL FO LC WC DA TG DA KI 
FB YG ZE UF AF AQ WL IB KL PB CL WL CB EZ IR CL WL UB TM YI CL EQ AF IX VL CN OD QW 

Im Folgenden wollen wir noch die Entschlüsselung mit dem FAIRPLAY-Kryptosystem an Hand eines historischen Chiffrats illustrieren.

Beispiel 3.14 (PLAYFAIR-Entschlüsselung)

Im 2. Weltkrieg sandte der spätere US-Präsident John F. Kennedy folgende mit dem Kennwort ROYAL NEW ZEALAND NAVY Playfair-verschlüsselte Nachricht ab []:

KXIEY UREBE ZWEHE WRYTU HEYFS
KREHE GOYFI WTTTU OLKSY CAIPO
BOTEI ZONTX BYBWT GONEY CUZWR
GDSON SXBOU YWRHE BAAHY USEDQ

Lässt man das Bigramm TT in der zweiten Zeile einfach stehen, da es als Playfair-Verschlüsselung nicht auftreten kann, so erhält man mit dem zum Passwort gehörigen PLAYFAIR-Quadrat

R O Y A L 
N E W Z D
V B C F G
H I K M P
Q S T U X

die Entschlüsselung:

PTBOA TONEO WENIN ELOST INACT
IONIN BLACK ETTST RAITT WOMIL 
ESSWM ERESU COCEX CREWO FTWEL
VEXRE QUEST ANYIN FORMA TIONX

was zu folgendem Klartext umgeschrieben wird:

PT BOAT ONE OWE NINE LOST IN ACTION IN BLACKETT STRAIT TWO MILES SW MERESU
COCE X CREW OF TWELVE X REQUEST ANY INFORMATION X

Statt MERESU COCE muss es wohl MERESU COVE heißen, also sollte an entsprechender Stelle im verschlüsselten Text eigentlich BN statt BW stehen.